题目内容
5.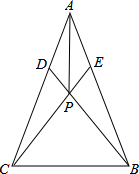 如图,△ABC中,D、E分别是AC、AB上的点,且CD=BE,BD、CE相交于点P,AP平分∠BAC,求证:AB=AC.
如图,△ABC中,D、E分别是AC、AB上的点,且CD=BE,BD、CE相交于点P,AP平分∠BAC,求证:AB=AC.
分析 作DG⊥BC于G,作EH⊥BC于H,作PM⊥AC于M,作PN⊥AB于N,先根据三角形面积相等求出DG=EH,利用全等三角形的判定定理即可得到△CGD≌△BHE,于是得到∠ABC=∠ACB,利用等角对等边即可得到AB=AC.
解答 证明:作DG⊥BC于G,作EH⊥BC于H,作PM⊥AC于M,作PN⊥AB于N,
∵AP平分∠BAC,
∴PM=PN,
∵CD=BE,
∴△CPD与△BPE的面积相等,
∴△BCD与△CBE的面积相等,
∴DG=EH,
又∵CD=BE,
∴△CGD≌△BHE,
∴∠ABC=∠ACB,
∴AB=AC.
点评 此题考查了全等三角形的判定与性质,角平分线定理,以及等腰三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
15.大、小两圆同心,环形面积是小圆面积的$\frac{a}{b}$倍,若大、小两圆的半径分别为R、r,则$\frac{R}{r}$等于( )
| A. | $\frac{\sqrt{a-b}}{\sqrt{b}}$ | B. | $\frac{\sqrt{a}}{\sqrt{a-b}}$ | C. | $\frac{\sqrt{b}}{\sqrt{a-b}}$ | D. | $\frac{\sqrt{a+b}}{\sqrt{b}}$ |
15. 如图,在?ABCD中,点E、F分别在AB、CD上,且AE=CF,则四边形BFDE不可能是( )
如图,在?ABCD中,点E、F分别在AB、CD上,且AE=CF,则四边形BFDE不可能是( )
 如图,在?ABCD中,点E、F分别在AB、CD上,且AE=CF,则四边形BFDE不可能是( )
如图,在?ABCD中,点E、F分别在AB、CD上,且AE=CF,则四边形BFDE不可能是( )| A. | 矩形 | B. | 菱形 | C. | 梯形 | D. | 平行四边形 |
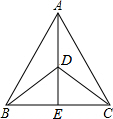 如图,在△ABC中,AB=AC,DB=DC,AD的延长线交BC于点E,求证:∠BAE=∠CAE.
如图,在△ABC中,AB=AC,DB=DC,AD的延长线交BC于点E,求证:∠BAE=∠CAE.
 如图,在△ABC中,∠CAE=45°,F是高AD与CE的交点,BE=4,则线段EF=4.
如图,在△ABC中,∠CAE=45°,F是高AD与CE的交点,BE=4,则线段EF=4.
 如图,当x=2时,抛物线y=ax2+bx+c取得最小值-1,并且抛物线与y轴交于点C(0,3),与x轴交于点A、B.
如图,当x=2时,抛物线y=ax2+bx+c取得最小值-1,并且抛物线与y轴交于点C(0,3),与x轴交于点A、B.