题目内容
15.大、小两圆同心,环形面积是小圆面积的$\frac{a}{b}$倍,若大、小两圆的半径分别为R、r,则$\frac{R}{r}$等于( )| A. | $\frac{\sqrt{a-b}}{\sqrt{b}}$ | B. | $\frac{\sqrt{a}}{\sqrt{a-b}}$ | C. | $\frac{\sqrt{b}}{\sqrt{a-b}}$ | D. | $\frac{\sqrt{a+b}}{\sqrt{b}}$ |
分析 利用圆的面积公式结合环形面积是小圆面积的$\frac{a}{b}$倍,得出大圆面积和小圆面积的面积关系进而求出即可.
解答 解:∵大、小两圆同心,环形面积是小圆面积的$\frac{a}{b}$倍,
∴大圆面积是小圆面积的:$\frac{a+b}{b}$倍,
则$\frac{π{R}^{2}}{π{r}^{2}}$=$\frac{a+b}{b}$,
∴$\frac{R}{r}$=$\frac{\sqrt{a+b}}{\sqrt{b}}$.
故选:D.
点评 此题主要考查了二次根式的应用,根据题意得出两圆的面积关系是解题关键.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
20.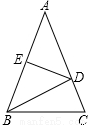 如图,在△ABC中,AB=AC=20cm,DE是AB的垂直平分线,若△BCD的周长为35cm,则BC的长为( )
如图,在△ABC中,AB=AC=20cm,DE是AB的垂直平分线,若△BCD的周长为35cm,则BC的长为( )
 如图,在△ABC中,AB=AC=20cm,DE是AB的垂直平分线,若△BCD的周长为35cm,则BC的长为( )
如图,在△ABC中,AB=AC=20cm,DE是AB的垂直平分线,若△BCD的周长为35cm,则BC的长为( )| A. | 15cm | B. | 10cm | C. | 8cm | D. | 5cm |
7.已知两个相似多边形的面积比是9:16,其中较小多边形的周长为36cm,则较大多边形的周长为( )
| A. | 48cm | B. | 54cm | C. | 56cm | D. | 64cm |
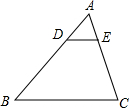 在△ABC中,DE∥BC,若$\frac{AD}{BD}=\frac{1}{2}$,
在△ABC中,DE∥BC,若$\frac{AD}{BD}=\frac{1}{2}$,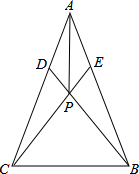 如图,△ABC中,D、E分别是AC、AB上的点,且CD=BE,BD、CE相交于点P,AP平分∠BAC,求证:AB=AC.
如图,△ABC中,D、E分别是AC、AB上的点,且CD=BE,BD、CE相交于点P,AP平分∠BAC,求证:AB=AC.