题目内容
如果抛物线y=
x2+(m-1)x-m+2的对称轴是y轴,那么m的值是 .
| 1 |
| 2 |
考点:二次函数的性质
专题:
分析:由对称轴是y轴可知一次项系数为0,可求得m的值.
解答:解:∵y=
x2+(m-1)x-m+2的对称轴是y轴,
∴m-1=0,解得m=1,
故答案为:1.
| 1 |
| 2 |
∴m-1=0,解得m=1,
故答案为:1.
点评:本题主要考查抛物线的对称轴,掌握抛物线的对称轴为y轴其一次项系数为0是解题的关键.

练习册系列答案
相关题目
抛物线y=-
x2的图象向右平移2个单位长度后所得新的抛物线的顶点坐标为( )
| 1 |
| 2 |
| A、(0,-2) |
| B、(0,2) |
| C、(-2,0) |
| D、(2,0) |
下列运算正确的是( )
| A、(x-y)2=x2-y2 |
| B、x6÷x2=x4 |
| C、x2y+xy2=x3y3 |
| D、x2•y2=(xy)4 |
下列判断错误的是( )
A、0•
| ||||||||||||
B、如果
| ||||||||||||
C、设
| ||||||||||||
D、如果|
|
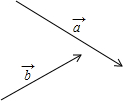 如图,已知两个不平行的向量
如图,已知两个不平行的向量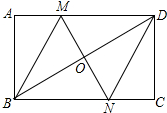 如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BD相交于点N,连接MB,ND.
如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BD相交于点N,连接MB,ND. 如图,在△ABC中,AD、BE分别是边BC、AC上的中线,AD、BE相交于G.设
如图,在△ABC中,AD、BE分别是边BC、AC上的中线,AD、BE相交于G.设