题目内容
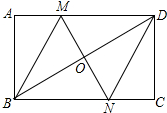 如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BD相交于点N,连接MB,ND.
如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BD相交于点N,连接MB,ND.(1)求证:四边形BMDN是菱形;
(2)若AB=1,AD=2,求MD的长.
考点:菱形的判定与性质,全等三角形的判定与性质,矩形的性质
专题:
分析:(1)根据矩形性质求出AD∥BC,推出∠MDO=∠NBO,∠DMO=∠BNO,证△DMO≌△BNO,推出OM=ON,得出平行四边形BMDN,推出菱形BMDN;
(2)根据菱形性质求出DM=BM,在Rt△AMB中,根据勾股定理得出BM2=AM2+AB2,推出x2=x2-32x+256+64,求出即可.
(2)根据菱形性质求出DM=BM,在Rt△AMB中,根据勾股定理得出BM2=AM2+AB2,推出x2=x2-32x+256+64,求出即可.
解答:(1)证明:∵四边形ABCD是矩形
∴AD∥BC,∠A=90°,
∴∠MDO=∠NBO,∠DMO=∠BNO,
在△DMO和△BNO中 ,
,
,
∴△DMO≌△BNO(ASA),
∴OM=ON,
∵OB=OD,
∴四边形BMDN是平行四边形,
∵MN⊥BD,
∴平行四边形BMDN是菱形.
(2)解:∵四边形BMDN是菱形,
∴MB=MD,
在Rt△AMB中,∵BM2=AM2+AB2
∴MD2=(2-MD)2+12,
解得:MD=
(舍去负值),
即:MD长为
.
∴AD∥BC,∠A=90°,
∴∠MDO=∠NBO,∠DMO=∠BNO,
在△DMO和△BNO中
 ,
,
|
∴△DMO≌△BNO(ASA),
∴OM=ON,
∵OB=OD,
∴四边形BMDN是平行四边形,
∵MN⊥BD,
∴平行四边形BMDN是菱形.
(2)解:∵四边形BMDN是菱形,
∴MB=MD,
在Rt△AMB中,∵BM2=AM2+AB2
∴MD2=(2-MD)2+12,
解得:MD=
| 5 |
| 4 |
即:MD长为
| 5 |
| 4 |
点评:本题考查了矩形性质,平行四边形的判定,菱形的判定和性质,勾股定理等知识点的应用,对角线互相平分的四边形是平行四边形,对角线互相垂直的平行四边形是菱形.

练习册系列答案
相关题目
如果两个相似三角形的面积比是1:6,则它们的相似比( )
| A、1:36 | ||
| B、1:6 | ||
| C、1:3 | ||
D、1:
|
某班体育委员记录了第一小组七位同学定点投篮(每人投10个)的情况.投进篮筐的个数分别为:7,10,5,3,4,9,4.则这组数据的平均数和众数分别是( )
| A、4,5 | B、5,4 |
| C、6,4 | D、5,6 |


 如图,斜坡AB的坡度i=1:3,该斜坡的水平距离AC=6米,那么斜坡AB的长等于
如图,斜坡AB的坡度i=1:3,该斜坡的水平距离AC=6米,那么斜坡AB的长等于