题目内容
1. 如图,已知△ABC中,AB=AC,D在BC上,连接AD,且AD=AE,若∠BAD=40°,求∠CDE的度数.
如图,已知△ABC中,AB=AC,D在BC上,连接AD,且AD=AE,若∠BAD=40°,求∠CDE的度数.
分析 首先得到△ABC,△ADE均为等腰三角形,再根据等腰三角形的性质求解.
解答 解:∵AB=AC,
∴△ABC为等腰三角形,
∵AD=AE,
∴△ADE为等腰三角形,
∵∠BAD=40°,
∴∠DAE=40°,
∴∠ADE=$\frac{1}{2}$(180°-∠DAE)=$\frac{1}{2}$(180°-40°)=70°,
又∵△ABC为等腰三角形,∵∠BAD=∠DAE,
∴AD⊥CD(三线合一),
∴∠CDE=90°-∠ADE=90°-70°=20°.
点评 本题主要考查等腰三角形的判定与性质,还涉及三角形内角和等知识点,需要熟练掌握等腰三角形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知在△ABC中,D、E分别为AB、AC中点,连接CD并延长至G,使CD=DG,连接AG;延长BE至 F,连接AF,使BE=AF.求证:AG=AF.
如图,已知在△ABC中,D、E分别为AB、AC中点,连接CD并延长至G,使CD=DG,连接AG;延长BE至 F,连接AF,使BE=AF.求证:AG=AF.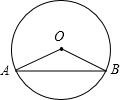 如图,AB是圆O的弦,若∠A=35°,则∠AOB的大小为110度.
如图,AB是圆O的弦,若∠A=35°,则∠AOB的大小为110度.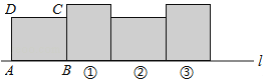 在矩形ABCD中,已知AB=4,BC=3,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2016次后,顶点A在整个旋转过程中所经过的路程之和是3024π.
在矩形ABCD中,已知AB=4,BC=3,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2016次后,顶点A在整个旋转过程中所经过的路程之和是3024π.