题目内容
4. 如图,以△ABC边AB为直径作⊙O交BC于D,已知AB=AC,
如图,以△ABC边AB为直径作⊙O交BC于D,已知AB=AC,(1)求证:BD=CD;
(2)若:∠A=36°,求弧AD的度数.
分析 (1)首先连接AD,由AB为直径,根据直径所对的圆周角是直角,可得AD⊥BC,又由AB=AC,根据三线合一的性质,可证得结论;
(2)由AB=AC,AD⊥BC,利用三线合一的性质,可求得∠BAD的度数,继而求得$\widehat{BD}$的度数,则可求得答案.
解答  (1)证明:连接AD,
(1)证明:连接AD,
∵AB为圆O的直径,
∴∠ADB=∠ADC=90°,
∵AB=AC,
∴BD=CD;
(2)解:∵AB=AC,∠ADB=90°,∠BAC=36°,
∴∠BAD=$\frac{1}{2}$∠BAC=18°,
∴弧BD=36°,
∴弧AD=180°-36°=144°.
点评 此题考查了圆周角定理以及等腰三角形的性质.注意掌握辅助线的作法是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.侧面展开图是一个长方形的几何体的是( )
| A. | 圆锥 | B. | 圆柱 | C. | 四棱柱 | D. | 球体 |
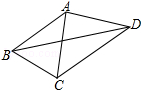 如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为88°.
如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为88°.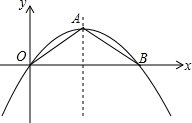 如图,抛物线的顶点为A(2,1),且经过原点O,与x轴的另一个交点为B.
如图,抛物线的顶点为A(2,1),且经过原点O,与x轴的另一个交点为B.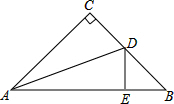 如图,在Rt△ABC中,已知∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若△BDE的周长为8,则AB的长为8.
如图,在Rt△ABC中,已知∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若△BDE的周长为8,则AB的长为8.