题目内容

14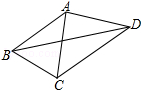．如图，已知AB=AC=AD，∠CBD=2∠BDC，∠BAC=44°，则∠CAD的度数为88°．

分析 由AB=AC=AD，可得B，C，D在以A为圆心，AB为半径的圆上，然后由圆周角定理，证得∠CAD=2∠CBD，∠BAC=2∠BDC，继而可得∠CAD=2∠BAC．

解答 解：∵AB=AC=AD，
∴B，C，D在以A为圆心，AB为半径的圆上，
∴∠CAD=2∠CBD，∠BAC=2∠BDC，
∵∠CBD=2∠BDC，∠BAC=44°，
∴∠CAD=2∠BAC=88°．
故答案为：88°．

点评 此题考查了圆周角定理．注意得到B，C，D在以A为圆心，AB为半径的圆上是解此题的关键．

练习册系列答案
相关题目
1．计算：
（1）$\sqrt{32}$-2$\sqrt{\frac{1}{3}}$+$\sqrt{48}$-$\sqrt{\frac{1}{8}}$；
（2）$\sqrt{8}$+$\sqrt{18}$-|-$\sqrt{2}$|；
（3）$\frac{1}{3}$$\sqrt{48x}$-11$\sqrt{x{y}^{4}}$-（$\frac{4}{x}$$\sqrt{3{x}^{3}}$-xy4$\sqrt{\frac{144}{x}}$）
2．已知开口向下的抛物线y=（k+1）x2+k2-16经过点（0，-7）．
（1）求k的值；
（2）点（-1，5）在这个函数的图象上吗？
2．如图，在等腰梯形ABCD中，AB∥DC，AB=16cm，CD=10cm，AD=5cm DE⊥AB，垂足为E，点P从点A出发，以2cm/秒的速度沿AB向终点B运动；点Q从点C出发，以1cm/秒的速度沿CD向终点D运动（P，Q两点中，有一个点运动到终点时，所有运动即终止），设P，Q同时出发并运动了t秒．

（1）当四边形EPQD为矩形时，求t的值；
（2）当以点E、P、C、Q为顶点的四边形是平行四边形时，求t的值；
（3）探索：是否存在这样的t值，使三角形PDQ是以PD为腰的等腰三角形？若存在，求出t的值；若不存在，请说明理由；
（4）在P、Q的运动过程中，当△PQB为钝角三角形时，请直接写出t的取值范围：$0≤t＜\frac{{2+\sqrt{73}}}{3}或\frac{13}{3}＜t≤8$．
9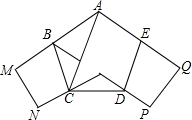．一条长为17.2cm、宽为2.5cm的长方形纸条，用如图的方法打一个结，然后轻轻拉紧、压平，就可以得到如图所示的正五边形ABCDE．若CN+DP=CD，四边形ACDE的面积是（　　）cm2．
A．$\frac{43}{6}$B．10．C．8.6D．$\frac{43}{3}$
19．把（-4）-（-6）-（+8）+（-9）写成省略加号的和的形式6-4-8-9．
6．根据下面给出的数轴，解答下面的问题：

（1）请根据图中A、B两点的位置，写出它们所表示的有理数A：1B：-2.5；
（2）观察数轴，与点A的距离为3的点表示的数是：4或-2；
（3）将数轴折叠，使A点与-3表示的点重合，则B点与数1.5表示的点重合．
3．已知（b+3）2+|a-2|=0，则ba的值是（　　）
A．-6B．6C．5D．1
4．如图，以△ABC边AB为直径作⊙O交BC于D，已知AB=AC，
（1）求证：BD=CD；
（2）若：∠A=36°，求弧AD的度数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网