题目内容
15．从长度分别为1、3、5、7的四条线段中任选三条作边，能构成三角形的概率为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{5}$ |
分析 从四条线段中任意选取三条，找出所有的可能，以及能构成三角形的情况数，即可求出所求的概率．
解答 解：从四条线段中任意选取三条，所有的可能有：1，3，5；1，3，7；1，5，7；3，5，7共4种，
其中构成三角形的有3，5，7共1种，
则P（构成三角形）=$\frac{1}{4}$．
故选C．
点评 此题考查了列表法与树状图法，以及三角形的三边关系，用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
5．下列各数中最大的数是（ ）
| A． | 5 | B． | $\sqrt{3}$ | C． | π | D． | -8 |
6．
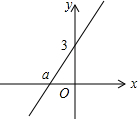如图，直线y=kx+b与y轴交于点（0，3）、与x轴交于点（a，0），当a满足-3≤a＜0时，k的取值范围是（ ）
如图，直线y=kx+b与y轴交于点（0，3）、与x轴交于点（a，0），当a满足-3≤a＜0时，k的取值范围是（ ）| A． | -1≤k＜0 | B． | 1≤k≤3 | C． | k≥1 | D． | k≥3 |
3．下列一元二次方程中有两个不相等的实数根的方程是（ ）
| A． | （x-1）2=0 | B． | x2+2x-19=0 | C． | x2+4=0 | D． | x2+x+l=0 |
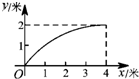
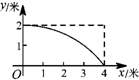
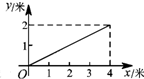
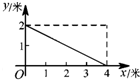
如图，以线段AB为直径作⊙O，CD与⊙O相切于点E，交AB的延长线于点D，连接BE，过点O作OC∥BE交切线DE于点C，连接AC．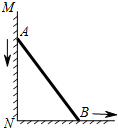
如图，一根长为5米的竹竿AB斜立于墙MN的右侧，底端B与墙角N 的距离为3米，当竹竿顶端A下滑x米时，底端B便随着向右滑行y米，反映y与x变化关系的大致图象是（ ）
