题目内容
1.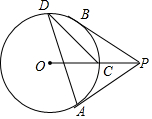 如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是优弧AB上不与点A、点B重合的一个动点,连接AD、CD,若∠APB=76°,则△ADC的度数为( )
如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是优弧AB上不与点A、点B重合的一个动点,连接AD、CD,若∠APB=76°,则△ADC的度数为( )| A. | 26° | B. | 20° | C. | 16° | D. | 30° |
分析 根据四边形的内角和,可得∠BOA,根据等弧所对的圆周角相等,根据圆周角定理,可得答案.
解答 解;如图, 连接OB、OA.
连接OB、OA.
∵PA、PB是⊙O的切线,
∴∠PBO=∠PAO=90°
由四边形的内角和定理,得
∠BOA=360°-90°-90°-76°=104°,
∵∠OPB=∠OPA,∠OPB+∠POB=90°,∠OPA+∠POA=90°,
∴∠POB=∠POA=52°.
∵∠ADC=$\frac{1}{2}$∠AOC=26°,
故选:A.
点评 本题考查了切线的性质、四边形的内角和定理、切线长定理、直角三角形的性质等知识,解题的关键啊灵活运用所学知识解决问题,学会添加常用辅助线,属于中考常考题型.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
11.对于任意实数k关于x的方程x2-kx-1=0根的情况为( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
12.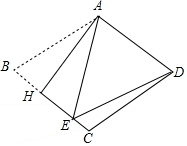 如图,把菱形ABCD沿AH折叠,B落在BC边上的点E处.若∠BAE=40°,则∠EDC的大小为( )
如图,把菱形ABCD沿AH折叠,B落在BC边上的点E处.若∠BAE=40°,则∠EDC的大小为( )
 如图,把菱形ABCD沿AH折叠,B落在BC边上的点E处.若∠BAE=40°,则∠EDC的大小为( )
如图,把菱形ABCD沿AH折叠,B落在BC边上的点E处.若∠BAE=40°,则∠EDC的大小为( )| A. | 10° | B. | 15° | C. | 18° | D. | 20° |
16.3的绝对值是( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
6.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (-a3)2=-a6 | C. | (-3a2)2=6a4 | D. | (-a+b)(a+b)=b2-a2 |
10.下列各数中无理数是( )
| A. | $\sqrt{4}$ | B. | 3.14 | C. | -π | D. | $\frac{22}{7}$ |
12.为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费,下表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信:(水价计费=自来水销售费用+污水处理费用)
已知小王家2012年4月份用水20吨,交水费66元;5月份用水25吨,交水费91元
(1)求a、b的值;
(2)6月份小王家用水32吨,应交水费多少元.
| 自来水销售价格 | 污水处理价格 | |
| 每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
| 17吨及以下 | a | 0.80 |
| 超过17吨不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
(1)求a、b的值;
(2)6月份小王家用水32吨,应交水费多少元.
 如果一条抛物线y=ax2+bx+c(a≠0)与x轴的两个交点为A,B(点A在点B的左侧),顶点为P,连接PA,PB,那么称△PAB为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴的两个交点为A,B(点A在点B的左侧),顶点为P,连接PA,PB,那么称△PAB为这条抛物线的“抛物线三角形”.