题目内容
8.有一个n位自然数$\overline{abcd…gh}$能被x0整除,依次轮换个位数字得到的新数$\overline{bcd…gha}$能被x0+1整除,再依次轮换个位数字得到的新数$\overline{cd…ghab}$能被x0+2整除,按此规律轮换后,$\overline{d…ghabc}$能被x0+3整除,…,$\overline{habc…g}$能被x0+n-1整除,则称这个n位数$\overline{abcd…gh}$是x0的一个“轮换数”.例如:60能被5整除,06能被6整除,则称两位数60是5的一个“轮换数”. 再如:324能被2整除,243能被3整除,432能被4整除,则称三位数324是2个一个“轮换数”.(1)请判断:自然数24是“轮换数”,245不是“轮换数”(填“是”或“不是”);
(2)若一个两位自然数的个位数字是m,十位数字是2m,求证:这个两位自然数一定是“轮换数”.
(3)若三位自然数$\overline{abc}$是4的一个“轮换数”,其中b<3,求这个三位自然数$\overline{abc}$.
分析 (1)分别判断能否被两个联系的整数整除即可;
(2)表示出这个两位自然数,和轮换两位自然数,得到能整除即可;
(3)先表示出三位自然数和轮换三位自然数,再根据能被5整除,得出b的可能值,进而用4整除,得出c的可能值,最后用能被3整除即可.
解答 解:(1)∵24是6的倍数,42是7的倍数,
∴自然数24是“轮换数”;
∵245的约数是5、7、7,452的约数有2、2、113;
当245被5整除时,而452不能被6整除;
当245被7整除时,而452不能被8
整除;
∴245不是“轮换数”.
(2)此两位数为20m+m=21m=7m×3,是3的倍数; 轮换后为10m+2m=12m=4m×4,是4的倍数;
∴这个两位自然数一定是“轮换数”.
(3)此三位数为:100a+10b+c
当b=0时,三位数为:100a+10b+c=100a+c,∵100a+c是4的倍数,而100a是4的倍数,
∴c是4的倍数,∴c=4或8;
若c=4,轮换后为40+a是5的倍数,∴a=5;
验证:再次轮换后为450是6的倍数,即这个三位数为:504
若c=8,则三位数为:100a+8;
轮换后为80+a是5的倍数,∴a=5;
验证:再次轮换后为850不是6的倍数,即c=8舍去
当b=1时,三位数为:100a+10+c,∵100a+10+c是4的倍数,而100a是4的倍数,
∴10+c是4的倍数,∴c=2或6;
若c=2,轮换后为100+20+a是5的倍数,∴a=5;
验证:再次轮换后为251不是6的倍数,即c=2舍去;
若c=6,轮换后为100+60+a是5的倍数,∴a=5;
验证:再次轮换后为651不是6的倍数,即c=6舍去
当b=2时,三位数为:100a+20+c,∵100a+20+c是4的倍数,而100a+20是4的倍数,
∴c是4的倍数,∴c=4或8;
若c=4,轮换后为200+40+a是5的倍数,∴a=5;
验证:再次轮换后为452不是6的倍数,即c=4舍去;
若c=8,轮换后为200+80+a是5的倍数,∴a=5;
验证:再次轮换后为852是6的倍数,即这个三位数为:528
综上所述,这个三位数为:504、528.
点评 此题是数的整除性,主要考查了3的倍数,4的倍数,5的倍数的特点,解本题的关键是用5的倍数求出b的值.

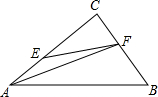 如图,在△ABC中,∠C=90°,AC=BC,且$\frac{AE}{EC}$=$\frac{CF}{FB}$=$\frac{1}{2}$.求证:∠CEF=∠FAB.
如图,在△ABC中,∠C=90°,AC=BC,且$\frac{AE}{EC}$=$\frac{CF}{FB}$=$\frac{1}{2}$.求证:∠CEF=∠FAB.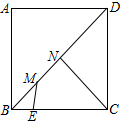 在边长为5正方形ABCD中,点E是BC上,且BE=2,点M、N是对角线BD上两点,且MN=$\sqrt{2}$.当四边形CEMN周长最小时,则cos∠BCN的值$\frac{4}{5}$.
在边长为5正方形ABCD中,点E是BC上,且BE=2,点M、N是对角线BD上两点,且MN=$\sqrt{2}$.当四边形CEMN周长最小时,则cos∠BCN的值$\frac{4}{5}$.