题目内容
15.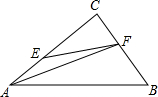 如图,在△ABC中,∠C=90°,AC=BC,且$\frac{AE}{EC}$=$\frac{CF}{FB}$=$\frac{1}{2}$.求证:∠CEF=∠FAB.
如图,在△ABC中,∠C=90°,AC=BC,且$\frac{AE}{EC}$=$\frac{CF}{FB}$=$\frac{1}{2}$.求证:∠CEF=∠FAB.
分析 过F作FG⊥AB,交AB于点G,则可证明△CEF∽△GAF,可证得结论.
解答  证明:
证明:
过F作FG⊥AB,交AB于点G,
∵AC=BC,且$\frac{AE}{EC}$=$\frac{CF}{FB}$=$\frac{1}{2}$,
∴不妨设CF=1,则BF=CE=2,CB=3,
∵∠C=90°,
∴∠B=45°,
∴FG=GB=$\frac{\sqrt{2}}{2}$BF=$\sqrt{2}$,
又AB=$\sqrt{2}$BC=3$\sqrt{2}$,
∴AG=AB-BG=3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$,
∴$\frac{CE}{AG}$=$\frac{2}{2\sqrt{2}}$=$\frac{1}{\sqrt{2}}$,$\frac{CF}{FG}$=$\frac{1}{\sqrt{2}}$,
∴$\frac{CE}{AG}$=$\frac{CF}{FG}$,且∠C=∠FGA,
∴△CEF∽△GAF,
∴∠CEF=∠FAB.
点评 本题主要考查相似三角形的判定和性质,构造三角形相似是解题的关键.

练习册系列答案
相关题目
5.P(3,-4)与点M(a,b)关于原点对称,则a+b的值为( )
| A. | -1 | B. | 1 | C. | 3 | D. | -4 |
 如图,在平面直角坐标系中,A(0,2),B(-2,4),C(-1,-2).试分别作出△ABC关于直线m:x=1和直线n;y=-1的对称图形,并写出对应顶点的坐标.
如图,在平面直角坐标系中,A(0,2),B(-2,4),C(-1,-2).试分别作出△ABC关于直线m:x=1和直线n;y=-1的对称图形,并写出对应顶点的坐标.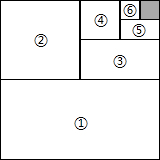 如图,将一个边长为1的正方形纸片分割成7个部分,部分②是部分①面积的一半,部分③是部分②面积的一半,依此类推.
如图,将一个边长为1的正方形纸片分割成7个部分,部分②是部分①面积的一半,部分③是部分②面积的一半,依此类推.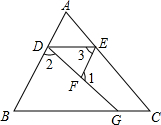 如图,D、E、F分别是直线AB、AC、DG上的点,已知∠1+∠2=180°,∠3=∠B,∠C=50°,求∠AED的度数.
如图,D、E、F分别是直线AB、AC、DG上的点,已知∠1+∠2=180°,∠3=∠B,∠C=50°,求∠AED的度数.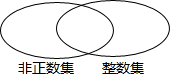 如图的两个圈分别表示非正数集和整数集,请在每个圈内填入六个数,其中三个数既在非正数集又在整数集内,你能用一个合适的语句来表示两个圈重叠部分的意义吗?
如图的两个圈分别表示非正数集和整数集,请在每个圈内填入六个数,其中三个数既在非正数集又在整数集内,你能用一个合适的语句来表示两个圈重叠部分的意义吗?