题目内容
6.计算:(2x+1)(3x+2)=6x2+7x+2;
(2x-2)(5x+3)=10x2-4x-6;
(x-4)(4x-3)=4x2-19x+12;
($\frac{1}{2}$x+1)($\frac{1}{2}$x-1)=$\frac{1}{4}$x2-1;
由此可得规律:(ax+b)(cx+d)=acx2+(ad+bc)x+bd.
分析 多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.依此即可求解.
解答 解:(2x+1)(3x+2)=6x2+7x+2;
(2x-2)(5x+3)=10x2-4x-6;
(x-4)(4x-3)=4x2-19x+12;
($\frac{1}{2}$x+1)($\frac{1}{2}$x-1)=$\frac{1}{4}$x2-1;
由此可得规律:(ax+b)(cx+d)=acx2+(ad+bc)x+bd.
故答案为:6x2+7x+2;10x2-4x-6;4x2-19x+12;$\frac{1}{4}$x2-1;acx2+(ad+bc)x+bd.
点评 本题主要考查了多项式乘多项式的运算,运用法则时应注意以下两点:
①相乘时,按一定的顺序进行,必须做到不重不漏;②多项式与多项式相乘,仍得多项式,在合并同类项之前,积的项数应等于原多项式的项数之积.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
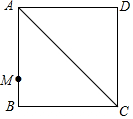 如图,正方形ABCD的边长为8cm,点M在AB上,BM=2cm,对角线AC有一个动点P,求PM+PB的最小值.
如图,正方形ABCD的边长为8cm,点M在AB上,BM=2cm,对角线AC有一个动点P,求PM+PB的最小值.