题目内容
20.Rt△ACB中,∠ACB=90°,AB=12,G为△ABC的重心,则CG=4.分析 在Rt△ABC中,∠C=90°,点G为重心,AB=12,则AB边上的中线是6,根据重心的性质即可求出CG.
解答 解:在Rt△ABC中,∠C=90°,
∵AB=12,
∴AB边上的中线是6,
∵点G为重心,
∴CG=6×$\frac{2}{3}$=4.
故答案是:4.
点评 本题主要考查了三角形的重心的性质,是需要熟记的内容.重心的性质:①重心到顶点的距离与重心到对边中点的距离之比为2:1;②重心和三角形3个顶点组成的3个三角形面积相等;③重心到三角形3个顶点距离的和最小(等边三角形).

练习册系列答案
相关题目
8.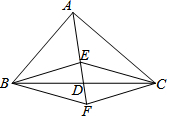 如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,DE=DF.在下列条件中,使四边形BECF是菱形的是( )
如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,DE=DF.在下列条件中,使四边形BECF是菱形的是( )
 如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,DE=DF.在下列条件中,使四边形BECF是菱形的是( )
如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,DE=DF.在下列条件中,使四边形BECF是菱形的是( )| A. | EB⊥EC | B. | AB⊥AC | C. | AB=AC | D. | BF∥CE |
12.下面调查中,适合采用普查的是( )
| A. | 调查你所在的班级同学的身高情况 | B. | 调查全国中学生心理健康现状 | ||
| C. | 调查我市食品合格情况 | D. | 调查中央电视台《少儿节目》收视率 |
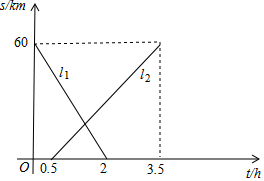 A,B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中l1,l2表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
A,B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中l1,l2表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题: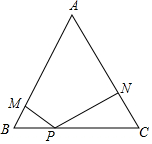 在边长为2的等边三角形ABC中,P是BC边上任意一点,过点 P分别作 PM⊥A B,PN⊥AC,M、N分别为垂足.
在边长为2的等边三角形ABC中,P是BC边上任意一点,过点 P分别作 PM⊥A B,PN⊥AC,M、N分别为垂足.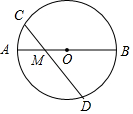 如图,AB是⊙O的直径,AB=4,点M是OA的中点,过点M的直线与⊙O交于C、D两点.若∠CMA=45°,则弦CD的长为$\sqrt{14}$.
如图,AB是⊙O的直径,AB=4,点M是OA的中点,过点M的直线与⊙O交于C、D两点.若∠CMA=45°,则弦CD的长为$\sqrt{14}$.