题目内容
9.已知某一次函数的图象经过点(0,-3),且与正比例函数y=$\frac{1}{2}$x的图象相交于点(2,a),求a的值及该一次函数的解析式.分析 把交点坐标代入正比例函数解析式计算即可求出m的值;将点(0,-3),(2,1)代入y=kx+b利用待定系数法即可求出一次函数解析式.
解答 解:∵点(2,a)在正比例函数y=$\frac{1}{2}$x的图象上,
∴a=2×$\frac{1}{2}$=1;
将点(0,-3),(2,1)代入y=kx+b得:
$\left\{\begin{array}{l}{b=-3}\\{2k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=-3}\end{array}\right.$,
∴此一次函数的解析式为:y=2x-3.
点评 本题考查了两直线相交问题,主要利用了一次函数图象上点的坐标特征,待定系数法求一次函数解析式,熟练掌握待定系数法是解题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 在△ABC中,AB=AC,AC边上的中线BD把三角形ABC的周长分为9cm和12cm的两部分,求三角形各边的长.
在△ABC中,AB=AC,AC边上的中线BD把三角形ABC的周长分为9cm和12cm的两部分,求三角形各边的长.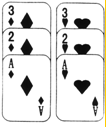 如图,是从一副扑克牌中取出的两组牌,分别是红桃1、2、3和方块1、2、3,将它们的背面朝上分别重新洗牌后,再从两组牌中各摸出一张,求摸出的两张牌的牌面数字之和小于5的概率.(要求用列表或树状图表示)
如图,是从一副扑克牌中取出的两组牌,分别是红桃1、2、3和方块1、2、3,将它们的背面朝上分别重新洗牌后,再从两组牌中各摸出一张,求摸出的两张牌的牌面数字之和小于5的概率.(要求用列表或树状图表示)