题目内容
14.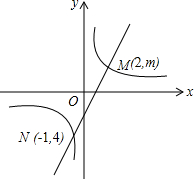 如图,一次函数y=ax+b的图象与反比例函数$y=\frac{k}{x}$的图象交于M(2,m)、N(-1,-4)两点.求:
如图,一次函数y=ax+b的图象与反比例函数$y=\frac{k}{x}$的图象交于M(2,m)、N(-1,-4)两点.求:(1)反比例函数与一次函数的解析式.
(2)根据图象写出反比例函数的值大于一次函数的值的x的取值范围.
(3)请在y轴上确定一点P,使得|MP-PN|的值最大,则P点坐标为(0,-10).
分析 (1)把点N的坐标代入反比例函数解析式可得k的值,把M的横坐标代入反比例函数解析式可得m的值,把M,N的坐标代入一次函数解析式可得a,b的值;
(2)根据图象上两个函数的交点即可得到结论;
(3)作N点关于y轴对称点N′,连接MN′,直线MN′与y轴交点即为P点,此时|PM-PN|最大,直线MN′与y轴的交点即为所求.
解答 解:(1)设反比例函数解析式为y=$\frac{k}{x}$,
把N的坐标代入得k=-1×(-4)=4,反比例函数解析式为 y=$\frac{4}{x}$,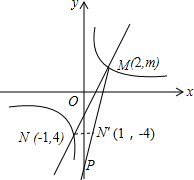
把M的坐标代入y=$\frac{4}{x}$得 2m=4,m=2,
把M的坐标代入y=ax+b得 2=2a+b
把N的坐标代入y=ax+b得-4=-a+b
解得a=2,b=-2.
∴一个函数的解析式为 y=2x-2;
(2)由图象知:0<x<2或x<-1,反比例函数的值大于一次函数的值;
(3)作N(-1,-4)关于y轴的对称点N′,连接MN′,直线MN′与y轴交点即为P点,此时|PM-PN|最大,
∵N(-1,-4),
∴N′(1,-4),
设直线MN′的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{-4=k+b}\\{2=2k+b}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=6}\\{b=-10}\end{array}\right.$,
令x=0,则y=-10,
∴P(0,-10).
故答案为:(0,-10).
点评 本题考查了利用函数的解析式求点的坐标,待定系数法求函数的解析式,求三角形的面积,最值问题,正确的作出辅助线是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.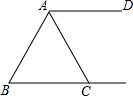 如图,AD∥BC,AC=BC,∠B=65°,则∠DAC的度数为( )
如图,AD∥BC,AC=BC,∠B=65°,则∠DAC的度数为( )
 如图,AD∥BC,AC=BC,∠B=65°,则∠DAC的度数为( )
如图,AD∥BC,AC=BC,∠B=65°,则∠DAC的度数为( )| A. | 50° | B. | 25° | C. | 60° | D. | 65° |
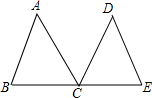 如图,已知:点C是线段BE的中点,AC平分∠DCB,CD平分∠ACE,AC=DC.
如图,已知:点C是线段BE的中点,AC平分∠DCB,CD平分∠ACE,AC=DC. 如图,在△ABC中,∠B=42°,将△ABC绕点A逆时针旋转至△ADE处,使点B落在BC的延长线上的D点处,则∠BDE的度数是84°.
如图,在△ABC中,∠B=42°,将△ABC绕点A逆时针旋转至△ADE处,使点B落在BC的延长线上的D点处,则∠BDE的度数是84°.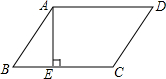 如图,平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,求平行四边形ABCD的周长.
如图,平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,求平行四边形ABCD的周长. 如图,有一斜坡AB长170m,坡顶离地面的高度BC为80m,求此斜坡的水平距离AC的长度.
如图,有一斜坡AB长170m,坡顶离地面的高度BC为80m,求此斜坡的水平距离AC的长度. 如图,CD是⊙O的直径,点A在DC的延长线上,∠A=20°,AE交⊙O于点B,且AB=OC.
如图,CD是⊙O的直径,点A在DC的延长线上,∠A=20°,AE交⊙O于点B,且AB=OC.