题目内容
关于x的一次函数y=kx-3的图象过点M(-2,1),则该图象与x轴交点坐标 ,与y轴交点坐标 .
考点:一次函数图象上点的坐标特征
专题:
分析:把点M的坐标代入一次函数即可求得k的值,然后让横坐标等于0得到图象与y轴的交点;让纵坐标等于0得到图象与y轴的交点.
解答:解:∵一次函数y=kx-3的图象经过点M(-2,1),
∴-2k-3=1.
解得:k=-2.
∴此一次函数的解析式为y=-2x-3.
令y=0,可得x=-
.
∴一次函数的图象与x轴的交点坐标为(-
,0).
令x=0,可得y=-3.
∴一次函数的图象与y轴的交点坐标为(0,-3).
故答案为(-
,0),(0,-3).
∴-2k-3=1.
解得:k=-2.
∴此一次函数的解析式为y=-2x-3.
令y=0,可得x=-
| 3 |
| 2 |
∴一次函数的图象与x轴的交点坐标为(-
| 3 |
| 2 |
令x=0,可得y=-3.
∴一次函数的图象与y轴的交点坐标为(0,-3).
故答案为(-
| 3 |
| 2 |
点评:本题考查的知识点是:在这条直线上的各点的坐标一定适合这条直线的解析式;x轴上的点纵坐标为0;y轴上的点横坐标为0.

练习册系列答案
相关题目
| 1 |
| 2 |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
点A(-3,2)关于x轴的对称点为点B,点B关于原点的对称点为C,则点C的坐标是( )
| A、(3,2) |
| B、(-3,2) |
| C、(3,-2) |
| D、(-2,3) |
下列各题中的两个项,不属于同类项的是( )
A、
| ||
| B、1与-32 | ||
| C、a2b与5×102ba2 | ||
D、2x2y与-
|
 在等腰△ABC中,AB=AC.求证:BC边上的高线,中线,∠A的角平分线互相重合.(提示:作BC边上的高AD)
在等腰△ABC中,AB=AC.求证:BC边上的高线,中线,∠A的角平分线互相重合.(提示:作BC边上的高AD)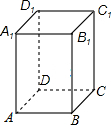 如图,有一个长、宽、高分别为2cm、2cm、3cm的长方体,有一只蚂蚁想沿着外侧壁从A点爬到C1处,请你帮助小蚂蚁计算出最短路线.
如图,有一个长、宽、高分别为2cm、2cm、3cm的长方体,有一只蚂蚁想沿着外侧壁从A点爬到C1处,请你帮助小蚂蚁计算出最短路线.