题目内容
 在等腰△ABC中,AB=AC.求证:BC边上的高线,中线,∠A的角平分线互相重合.(提示:作BC边上的高AD)
在等腰△ABC中,AB=AC.求证:BC边上的高线,中线,∠A的角平分线互相重合.(提示:作BC边上的高AD)考点:等腰三角形的性质
专题:证明题
分析:过点A作AD⊥BC于D,利用“HL”证明Rt△ABD和Rt△ACD全等,再根据全等三角形对应边相等可得BD=CD,全等三角形对应角相等可得∠BAD=∠CAD.
解答: 证明:如图,过点A作AD⊥BC于D,
证明:如图,过点A作AD⊥BC于D,
在Rt△ABD和Rt△ACD中,
,
∴Rt△ABD≌Rt△ACD(HL),
∴BD=CD,∠BAD=∠CAD,
故BC边上的高线,中线,∠A的角平分线互相重合.
 证明:如图,过点A作AD⊥BC于D,
证明:如图,过点A作AD⊥BC于D,在Rt△ABD和Rt△ACD中,
|
∴Rt△ABD≌Rt△ACD(HL),
∴BD=CD,∠BAD=∠CAD,
故BC边上的高线,中线,∠A的角平分线互相重合.
点评:本题考查了等腰三角形的性质的证明,难点在于作辅助线构造出全等三角形.

练习册系列答案
相关题目
估算
-2的值在( )
| 45 |
| A、在5和6之间 |
| B、在4和5之间 |
| C、在3和4之间 |
| D、在2和3之间 |
下列图形中,是圆周角的是( )
A、 |
B、 |
C、 |
D、 |
二次函数y=-3(x+1)2+2的图象的顶点坐标是( )
| A、(-1,8) |
| B、(1,8) |
| C、(-1,2) |
| D、(1,-4) |
 如图所示,在⊙O中弦BD=CE,求证:AB=AC.
如图所示,在⊙O中弦BD=CE,求证:AB=AC. 如图,OD是⊙O的半径,弦AB⊥OD于点C,连接BO并延长交⊙O于点E,连接EC,AE.若AB=8,CD=2,求CE的长.
如图,OD是⊙O的半径,弦AB⊥OD于点C,连接BO并延长交⊙O于点E,连接EC,AE.若AB=8,CD=2,求CE的长.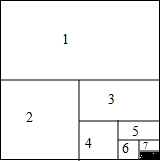 如图,将一个边长为1的正方形纸片分割成8部分,部分1是边长为1的正方形纸片的一半,部分2是部分1面积的一半,部分3是部分2面积的一半,依此类推.
如图,将一个边长为1的正方形纸片分割成8部分,部分1是边长为1的正方形纸片的一半,部分2是部分1面积的一半,部分3是部分2面积的一半,依此类推.