题目内容
按规定的方法解下列方程:
(1)(x+1)2-144=0(直接开平方法);
(2)x2=8x+9(配方法);
(3)2y2+7y+3=0(公式法);
(4)3(x-2)2=x(x-2)(因式分解法).
(1)(x+1)2-144=0(直接开平方法);
(2)x2=8x+9(配方法);
(3)2y2+7y+3=0(公式法);
(4)3(x-2)2=x(x-2)(因式分解法).
考点:解一元二次方程-因式分解法,解一元二次方程-直接开平方法,解一元二次方程-配方法,解一元二次方程-公式法
专题:
分析:(1)移项,然后开平方即可求解;
(2)首先移项,然后配方,利用直接开平方法即可求解;
(3)利用公式法即可求解;
(4)移项,然后利用因式分解法即可求解.
(2)首先移项,然后配方,利用直接开平方法即可求解;
(3)利用公式法即可求解;
(4)移项,然后利用因式分解法即可求解.
解答:解:(1)(x+1)2=144,
则x+1=12或x+1=-12,
解得:x1=-13,x2=11;
(2)移项,得:x2-8x=9,
配方,得x2-8x+16=25,
则(x-4)2=±5,
即x-4=5或x-4=-5,
解得:x1=9,x2=-1;
(3)a=2,b=7,c=3,
△=49-4×2×3=49-24=25>0.
则x=
,
则x1=-3,x2=-
;
(4)原式即3(x-2)2-x(x-2)=0,
因式分解得:(x-2)【3(x-2)-x】=0,
即(x-2)(2x-6)=0,
则x-2=0或2x-6=0,
解得:x1=2,x2=3.
则x+1=12或x+1=-12,
解得:x1=-13,x2=11;
(2)移项,得:x2-8x=9,
配方,得x2-8x+16=25,
则(x-4)2=±5,
即x-4=5或x-4=-5,
解得:x1=9,x2=-1;
(3)a=2,b=7,c=3,
△=49-4×2×3=49-24=25>0.
则x=
| -7±5 |
| 4 |
则x1=-3,x2=-
| 1 |
| 2 |
(4)原式即3(x-2)2-x(x-2)=0,
因式分解得:(x-2)【3(x-2)-x】=0,
即(x-2)(2x-6)=0,
则x-2=0或2x-6=0,
解得:x1=2,x2=3.
点评:本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
已知圆O的半径是6,点P到圆心的距离是4,则点P( )
| A、在圆外 | B、在圆上 |
| C、在圆内 | D、不确定 |
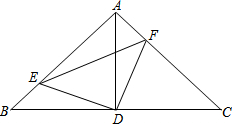 如图,在Rt△ABC中,AB=AC,∠BAC=90°,D为BC的中点.
如图,在Rt△ABC中,AB=AC,∠BAC=90°,D为BC的中点.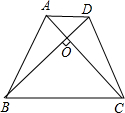 如图,已知在等腰梯形ABCD中,AD∥BC,AC⊥BD,且梯形ABCD的面积为100cm2,求梯形的高.
如图,已知在等腰梯形ABCD中,AD∥BC,AC⊥BD,且梯形ABCD的面积为100cm2,求梯形的高. 已知D、E、F分别为△ABC的三边BC、CA、AB边上的一点,且CE=BF,S△DCE=S△DBF.求证:AD平分∠BAC.
已知D、E、F分别为△ABC的三边BC、CA、AB边上的一点,且CE=BF,S△DCE=S△DBF.求证:AD平分∠BAC.