题目内容
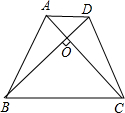 如图,已知在等腰梯形ABCD中,AD∥BC,AC⊥BD,且梯形ABCD的面积为100cm2,求梯形的高.
如图,已知在等腰梯形ABCD中,AD∥BC,AC⊥BD,且梯形ABCD的面积为100cm2,求梯形的高.考点:等腰梯形的性质
专题:
分析:运用等腰梯形的面积等于对角线乘积的一半,求出对角线的长,再运用△AOD和△BOC是等腰直角三角形,求出上底加下底的长,利用公式即可求出梯形的高.
解答:解:∵AC⊥BD,梯形的面积为100cm2,
∴
AC•BD=100,
∵等腰梯形ABCD的对角形相等,即AC=BD,
∴AC=10
cm,
∵△AOD和△BOC是等腰直角三角形,
∴AD=
AO,BC=
OC,
∴AD+BC=
(AO+CO)=
AC=20cm,
∵梯形的面积=
×(AD+BC)×h,
∴100=
×20×h,
解得h=10cm,
∴梯形的高为10cm.
∴
| 1 |
| 2 |
∵等腰梯形ABCD的对角形相等,即AC=BD,
∴AC=10
| 2 |
∵△AOD和△BOC是等腰直角三角形,
∴AD=
| 2 |
| 2 |
∴AD+BC=
| 2 |
| 2 |
∵梯形的面积=
| 1 |
| 2 |
∴100=
| 1 |
| 2 |
解得h=10cm,
∴梯形的高为10cm.
点评:本题主要考查了等腰梯形的性质,解题的关键是运用当对角线垂直的等腰梯形的面积等于对角线乘积的一半.

练习册系列答案
相关题目
学校、小明家、书店依次座落在一条东西走向的大街上,学校在小明家的正东2千米,书店在小明家的正西10千米.规定向东走为正.小明骑车从家出发,向西走了5千米,接着又向东走了-5千米,此时张明的位置在( )
| A、学校 | B、家 |
| C、书店 | D、以上都不对 |
过多边形的一个顶点可以引出6条对角线,则多边形的边数是( )
| A、7 | B、8 | C、9 | D、10 |
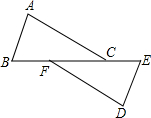 如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,AB=DE.求证:FB=CE.
如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,AB=DE.求证:FB=CE. 八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,设直线l和八个正方形的最上面交点为A,则A的坐标是
八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,设直线l和八个正方形的最上面交点为A,则A的坐标是 如图,在△ABC中,AB=AC,D为△ABC内一点,且∠1=∠2,若∠A=50°,则∠BDC=
如图,在△ABC中,AB=AC,D为△ABC内一点,且∠1=∠2,若∠A=50°,则∠BDC=