题目内容
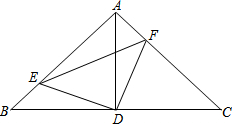 如图,在Rt△ABC中,AB=AC,∠BAC=90°,D为BC的中点.
如图,在Rt△ABC中,AB=AC,∠BAC=90°,D为BC的中点.(1)求证:DA=DB=DC;
(2)若E、F分别时线段AB、AC上的点,且AF=BE,试判断△DEF的形状,并说明理由.
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)根据中线定义和自己三角形斜边上的中线性质求出即可.
(2)根据直角三角形性质和等腰三角形性质求出∠FAD=∠B=∠C=∠EAD=45°,AD⊥BC,证△EBD≌△FAD,推出DE=DF,∠BED=∠ADF,求出∠EDF=∠ADB=90°,即可得出答案.
(2)根据直角三角形性质和等腰三角形性质求出∠FAD=∠B=∠C=∠EAD=45°,AD⊥BC,证△EBD≌△FAD,推出DE=DF,∠BED=∠ADF,求出∠EDF=∠ADB=90°,即可得出答案.
解答:(1)证明:∵在Rt△ABC中,AB=AC,∠BAC=90°,D为BC的中点.
∴DB=DC
BC,DA=
BC,
∴DA=DB=DC;
(2)解:△DEF是等腰直角三角形,
理由是:∵在Rt△ABC中,AB=AC,∠BAC=90°,D为BC的中点,
∴∠FAD=∠B=∠C=∠EAD=45°,AD⊥BC,
∴∠ADB=90°,
在△EBD和△FAD中
∴△EBD≌△FAD,
∴DE=DF,∠BED=∠ADF,
∴∠EDF=∠EDA+∠ADF=∠EDA+∠EDB=∠ADB=90°,
即△EDF是等腰三角形三角形.
∴DB=DC
| 1 |
| 2 |
| 1 |
| 2 |
∴DA=DB=DC;
(2)解:△DEF是等腰直角三角形,
理由是:∵在Rt△ABC中,AB=AC,∠BAC=90°,D为BC的中点,
∴∠FAD=∠B=∠C=∠EAD=45°,AD⊥BC,
∴∠ADB=90°,
在△EBD和△FAD中
|
∴△EBD≌△FAD,
∴DE=DF,∠BED=∠ADF,
∴∠EDF=∠EDA+∠ADF=∠EDA+∠EDB=∠ADB=90°,
即△EDF是等腰三角形三角形.
点评:本题考查了全等三角形的性质和判定,等腰三角形的性质,直角三角形的性质,等腰直角三角形的判定的应用,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
 如图,已知直线BC切⊙O于点C,PD为⊙O的直径,BP的延长线与CD的延长线交于点A,∠A=28°,∠B=26°,则∠PDC=( )
如图,已知直线BC切⊙O于点C,PD为⊙O的直径,BP的延长线与CD的延长线交于点A,∠A=28°,∠B=26°,则∠PDC=( )| A、34° | B、36° |
| C、38° | D、40° |
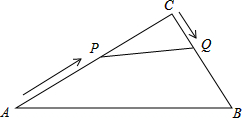 在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm,现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动,如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求:
在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm,现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动,如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求: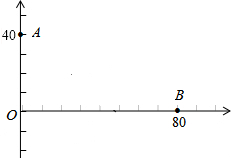 我海军某部发现,一艘敌舰从我岛屿O正东方向80海里的B处,沿东西方向向岛屿O驶来,指挥部立即下命令在岛屿O正北40海里A处的我军军舰沿直线前往拦截.若敌我两舰行驶速度相同,在上述坐标系中标出我舰最快截住敌舰的位置,并求出该点的坐标.
我海军某部发现,一艘敌舰从我岛屿O正东方向80海里的B处,沿东西方向向岛屿O驶来,指挥部立即下命令在岛屿O正北40海里A处的我军军舰沿直线前往拦截.若敌我两舰行驶速度相同,在上述坐标系中标出我舰最快截住敌舰的位置,并求出该点的坐标.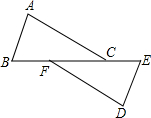 如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,AB=DE.求证:FB=CE.
如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,AB=DE.求证:FB=CE. 八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,设直线l和八个正方形的最上面交点为A,则A的坐标是
八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,设直线l和八个正方形的最上面交点为A,则A的坐标是