题目内容
14．已知a（a-1）-（a2-b）=1，求$\frac{1}{2}（{a}^{2}+{b}^{2}）-ab$的值$\frac{1}{2}$．分析 已知等式整理求出a-b的值，原式提取公因式，再利用完全平方公式化简，将a-b的值代入计算即可求出值．
解答 解：∵a（a-1）-（a2-b）=a2-a-a2+b=1，
∴a-b=-1，
则原式=$\frac{1}{2}$（a2+b2-2ab）=$\frac{1}{2}$（a-b）2=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．
点评 此题考查了因式分解-运用公式法，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
相关题目
5．下列运算正确的是（ ）
| A． | $\frac{{a}^{2}-{b}^{2}}{（a-b）^{2}}=\frac{a+b}{a-b}$ | B． | $\frac{{a}^{2}-{b}^{2}}{{a}^{2}+{b}^{2}}=\frac{a-b}{a+b}$ | ||
| C． | $\frac{x-1}{1-{x}^{2}}=\frac{1}{x+1}$ | D． | $\frac{-x-y}{-x+y}=\frac{x-y}{x+y}$ |
2．将下列多项式因式分解，结果中不含因式x-1的是（ ）
| A． | x2-1 | B． | x（x-2）+（2-x） | C． | x2-2 | D． | x2-2x+1 |
9．下列分解因式正确的是（ ）
| A． | m4-8m2+64=（m2-8）2 | B． | x4-y4=（x2+y2）（x2-y2） | ||
| C． | 4a2-4a+1=（2a-1）2 | D． | a（x-y）-b（y-x）=（x-y）（a-b） |
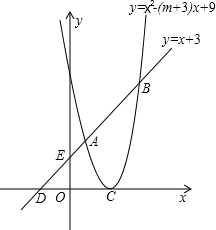如图，已知抛物线y=x2-（m+3）x+9的顶点C在x轴正半轴上，一次函数y=x+3与抛物线交于A、B两点，与x、y轴交于D、E两点．