题目内容
8.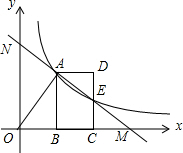 如图,O为原点,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,作AB⊥x轴于点B,点A的坐标为(2,3).
如图,O为原点,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,作AB⊥x轴于点B,点A的坐标为(2,3).(1)反比例函数的解析式为y=$\frac{6}{x}$(x>0);
(2)将线段AB沿x轴正方向平移到线段DC的位置,反比例函数y=$\frac{k}{x}$(x>0)的图象恰好经过DC的中点E,
①求直线AE的函数表达式;
②若直线AE与x轴交于点M,与y轴交于点N,请你写出线段AN与线段ME的大小,并说明理由.
分析 (1)由点A的坐标利用反比例函数图象上点的坐标特征可求出k值,从而得出反比例函数解析式;
(2)根据点E为CD的中点,可找出点E的纵坐标,结合点E在反比例函数图象上即可求出点E的坐标,再由点A、E的坐标利用待定系数法即可求出直线AE的函数表达式;
(3)AN=ME,根据直线AE的函数表达式可求出点M的坐标,结合点A、E的坐标可得出点B、C的坐标,由此即可得知:点B、C为线段OM的三等分点,再结合平行线的性质即可得出点A、E为线段MN的三等分点,由此即可得出结论.
解答 解:(1)∵点A(2,3)在反比例函数y=$\frac{k}{x}$(x>0)的图象上,
∴k=2×3=6,
∴反比例函数的解析式为y=$\frac{6}{x}$(x>0).
故答案为:y=$\frac{6}{x}$(x>0).
(2)∵AB=CD,点E为线段CD的中点,
∴点E的纵坐标为$\frac{3}{2}$,
将y=$\frac{3}{2}$代入y=$\frac{6}{x}$中,则有$\frac{3}{2}$=$\frac{6}{x}$,
解得:x=4,
∴点E的坐标为(4,$\frac{3}{2}$).
设直线AE的表达式为y=mx+n,
将点A(2,3)、E(4,$\frac{3}{2}$)代入y=mx+n中得:$\left\{\begin{array}{l}{3=2m+n}\\{\frac{3}{2}=4m+n}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=-\frac{3}{4}}\\{n=\frac{9}{2}}\end{array}\right.$,
∴直线AE的表达式为y=-$\frac{3}{4}$x+$\frac{9}{2}$.
(3)AN=ME,利用如下:
令y=-$\frac{3}{4}$x+$\frac{9}{2}$中y=0,则0=-$\frac{3}{4}$x+$\frac{9}{2}$,
解得:x=6,
∴点M的坐标为(6,0).
∵点A(2,3)、E(4,$\frac{3}{2}$),
∴点B(2,0),点C(4,0),
∴点B、C为线段OM的三等分点,
∵AB∥CD(平移的性质),
∴点A、E为线段MN的三等分点,
∴AN=ME.
点评 本题考查了反比例函数与一次函数的交点问题、待定系数法求函数解析式以及平行线的性质,解题的关键是:(1)利用反比例函数图象上点的坐标特征求出k值;(2)求出点E的坐标;(3)找出点A、E为线段MN的三等分点,本题属于中档题,难度不大,解决该题型题目时,找出点的坐标,再利用待定系数法求出函数解析式是关键.

| A. | 打开电视,正在播放《大国工匠》 | |
| B. | 袋中只有10个球,且都是红球,任意摸出一个球是红球 | |
| C. | 5年后数学课代表会考上清华大学 | |
| D. | 2015年全年由367天 |
| A. | $\sqrt{2}$+$\sqrt{2}$=2 | B. | $\sqrt{3}$-$\sqrt{3}$=0 | C. | $\sqrt{2}$×$\sqrt{2}$=4 | D. | $\sqrt{(-3)^{2}}$=-3 |
 如图,在?ABCD中,F是BC上的点,直线DF与AB的延长线相交于点E,与AC相交于点M,BP∥DF,且与AD相交于点P,与AC相交于点N,则图中的相似三角形有16对.
如图,在?ABCD中,F是BC上的点,直线DF与AB的延长线相交于点E,与AC相交于点M,BP∥DF,且与AD相交于点P,与AC相交于点N,则图中的相似三角形有16对.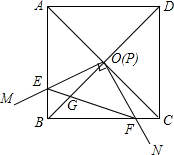 如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是(1),(2),(3),(5).
如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是(1),(2),(3),(5).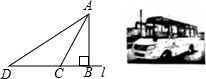 如图是我市投入使用的“大鼻子”校车,其安全隐患主要是超速和超载,某中学九年级数学活动小组设计了如下检测公路上行驶汽车速度的实验,先在笔直的车道l旁边选取一点A,再在l上确定点B,使AB⊥l,测得AB的长为30米,又在l上选取点C,D,使∠CAB=30°,∠DAB=60°,如图所示.
如图是我市投入使用的“大鼻子”校车,其安全隐患主要是超速和超载,某中学九年级数学活动小组设计了如下检测公路上行驶汽车速度的实验,先在笔直的车道l旁边选取一点A,再在l上确定点B,使AB⊥l,测得AB的长为30米,又在l上选取点C,D,使∠CAB=30°,∠DAB=60°,如图所示.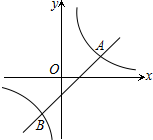 如图,已知A(4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点
如图,已知A(4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点