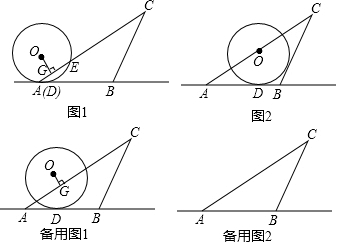
题目内容
13.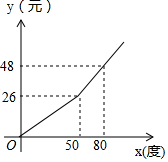 某城市电业局为鼓励居民节约用电,采取按月用电量分段收费办法,居民应交电费y(元)与用电量x(度)的函数关系如图所示.
某城市电业局为鼓励居民节约用电,采取按月用电量分段收费办法,居民应交电费y(元)与用电量x(度)的函数关系如图所示.(1)分别求出当0≤x<50和x≥50时,y与x的函数关系式;
(2)若某居民该月用电65度,则应交电费多少元?
分析 (1)对0≤x≤100段,列出正比例函数y=kx,对x≥100段,列出一次函数y=kx+b;将坐标点代入即可求出.
(2)根据(1)的函数解析式即可解答即可.
解答 解:(1)当0≤x≤50时.图象经过(0,0),(50,26).可设y=kx.
50k=26,
解得k=$\frac{13}{25}$,
∴y=$\frac{13}{25}$x(0≤x≤50).
当x≥50时.图象经过(50,26).(80,48),可设y=kx+b.
则有$\left\{\begin{array}{l}{50k+b=26}\\{80k+b=48}\end{array}\right.$解得$\left\{\begin{array}{l}{k=\frac{11}{15}}\\{b=-\frac{32}{3}}\end{array}\right.$,
∴y=$\frac{11}{15}$x-$\frac{32}{3}$.
(2)当x=65时,65>50,y=$\frac{11}{15}$×65-$\frac{32}{3}$=37.
答:该用户应交电费37元
点评 本题主要考查一次函数的应用待定系数法等知识,关键考查从一次函数的图象上获取信息的能力.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
9. 如图所示,下列说法正确的是( )
如图所示,下列说法正确的是( )
 如图所示,下列说法正确的是( )
如图所示,下列说法正确的是( )| A. | ∠1和∠2是内错角 | B. | ∠1和∠5是同位角 | ||
| C. | ∠1和∠2是同旁内角 | D. | ∠1和∠4是内错角 |
1.某班在一次数学测验后成绩统计如下表:
如果60分及以上为及格,那么这次数学测验的及格率是90%.
| 分数段(分) | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 | 90-100 |
| 人数 | 1 | 3 | 4 | 8 | 13 | 11 |
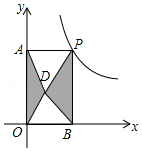 如图,点P是反比例函数y=$\frac{6}{x}$(x>0)的图象上的任意一点,过点P分别作两坐标轴的垂线,与坐标轴构成矩形OAPB,点D是矩形OAPB内任意一点,连接DA、DB、DP、DO,则图中阴影部分的面积是3.
如图,点P是反比例函数y=$\frac{6}{x}$(x>0)的图象上的任意一点,过点P分别作两坐标轴的垂线,与坐标轴构成矩形OAPB,点D是矩形OAPB内任意一点,连接DA、DB、DP、DO,则图中阴影部分的面积是3.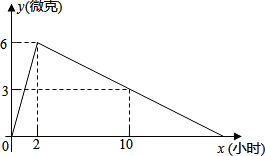 某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克,接着逐步衰减,10小时血液中含药量为每毫升3微克,每毫升血液中含药量y微克随时间x小时主变化如图所示,当成人按规定剂是服药后,
某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克,接着逐步衰减,10小时血液中含药量为每毫升3微克,每毫升血液中含药量y微克随时间x小时主变化如图所示,当成人按规定剂是服药后,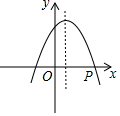 如图,抛物线y=ax2+bx+c(a<0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(3,0)在该抛物线上,则a-b+c的值为0.
如图,抛物线y=ax2+bx+c(a<0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(3,0)在该抛物线上,则a-b+c的值为0.