题目内容
19.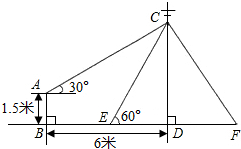 如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,则拉线CE的长为( )(结果保留小数点后一位,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73).
如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,则拉线CE的长为( )(结果保留小数点后一位,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73).| A. | 5.4 | B. | 5.7 | C. | 6.1 | D. | 6.3 |
分析 由题意可先过点A作AH⊥CD于H.在Rt△ACH中,可求出CH,进而CD=CH+HD=CH+AB,再在Rt△CED中,求出CE的长.
解答 解:过点A作AH⊥CD,垂足为H,
由题意可知四边形ABDH为矩形,∠CAH=30°,
∴AB=DH=1.5,BD=AH=6,
在Rt△ACH中,tan∠CAH=$\frac{CH}{AH}$,
∴CH=AH•tan∠CAH,
∴CH=AH•tan∠CAH=6tan30°=6×$\frac{\sqrt{3}}{3}$=2$\sqrt{3}$(米),
∵DH=1.5,
∴CD=2 $\sqrt{3}$+1.5,
在Rt△CDE中,
∵∠CED=60°,sin∠CED=$\frac{CD}{CE}$,
∴CE=$\frac{CD}{sin60°}$=4+$\sqrt{3}$≈5.7(米),
答:拉线CE的长约为5.7米,
故选B.
点评 本体考查了解直角三角形的应用--仰角俯角问题.要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
10.能用平方差公式计算的是( )
| A. | (-x+2y)(x-2y) | B. | (2x-y)(2y+x) | C. | (m-n)(n-m) | D. | 99×101 |
14. 先阅读材料再回答问题:如图线段AB=4,AC=1,BD=2,且AC⊥AB,BD⊥AB,点P在线段AB上运动,当AP=a时,则BP=4-a,PC=$\sqrt{1{+a}^{2}}$,PD=$\sqrt{4{+(4-a)}^{2}}$,由此可求得CP+DP的最小值为5.那么请问:代数式$\sqrt{4{+x}^{2}}$+$\sqrt{16{+(5-x)}^{2}}$的最小值为( )
先阅读材料再回答问题:如图线段AB=4,AC=1,BD=2,且AC⊥AB,BD⊥AB,点P在线段AB上运动,当AP=a时,则BP=4-a,PC=$\sqrt{1{+a}^{2}}$,PD=$\sqrt{4{+(4-a)}^{2}}$,由此可求得CP+DP的最小值为5.那么请问:代数式$\sqrt{4{+x}^{2}}$+$\sqrt{16{+(5-x)}^{2}}$的最小值为( )
 先阅读材料再回答问题:如图线段AB=4,AC=1,BD=2,且AC⊥AB,BD⊥AB,点P在线段AB上运动,当AP=a时,则BP=4-a,PC=$\sqrt{1{+a}^{2}}$,PD=$\sqrt{4{+(4-a)}^{2}}$,由此可求得CP+DP的最小值为5.那么请问:代数式$\sqrt{4{+x}^{2}}$+$\sqrt{16{+(5-x)}^{2}}$的最小值为( )
先阅读材料再回答问题:如图线段AB=4,AC=1,BD=2,且AC⊥AB,BD⊥AB,点P在线段AB上运动,当AP=a时,则BP=4-a,PC=$\sqrt{1{+a}^{2}}$,PD=$\sqrt{4{+(4-a)}^{2}}$,由此可求得CP+DP的最小值为5.那么请问:代数式$\sqrt{4{+x}^{2}}$+$\sqrt{16{+(5-x)}^{2}}$的最小值为( )| A. | 10 | B. | 2$\sqrt{10}$ | C. | $\sqrt{61}$ | D. | $\sqrt{41}$ |
4.下列各式表示正确的是( )
| A. | $\sqrt{25}=±5$ | B. | $±\sqrt{25}=5$ | C. | $±\sqrt{{{(-5)}^2}}=-5$ | D. | $±\sqrt{25}=±5$ |
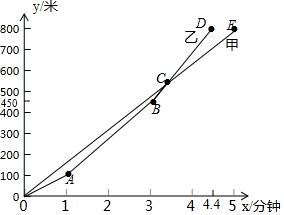 百舸竞渡,激情飞扬.为纪念爱国诗人屈原,某市举行龙舟赛.甲、乙两支龙舟队在比赛时,路程y(米)与时间x(分钟)之间的函数图象如图所示,根据图象回答下列问题:
百舸竞渡,激情飞扬.为纪念爱国诗人屈原,某市举行龙舟赛.甲、乙两支龙舟队在比赛时,路程y(米)与时间x(分钟)之间的函数图象如图所示,根据图象回答下列问题: