题目内容
9.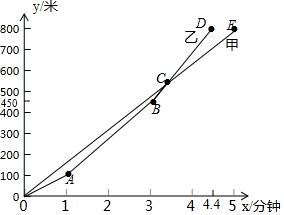 百舸竞渡,激情飞扬.为纪念爱国诗人屈原,某市举行龙舟赛.甲、乙两支龙舟队在比赛时,路程y(米)与时间x(分钟)之间的函数图象如图所示,根据图象回答下列问题:
百舸竞渡,激情飞扬.为纪念爱国诗人屈原,某市举行龙舟赛.甲、乙两支龙舟队在比赛时,路程y(米)与时间x(分钟)之间的函数图象如图所示,根据图象回答下列问题:(1)最先达到终点的是乙队,比另一对早0.6分钟到达;
(2)在比赛过程中,乙队在第1分钟和第3分钟时两次加速;
(3)求在什么时间范围内,甲队领先?
(4)相遇前,甲乙两队之间的距离不超过30m的时间范围是0<x≤0.5或3≤x≤$\frac{10}{3}$.
分析 (1)根据函数图象可以直接得到谁先到达终点和早到多长时间;
(2)根据函数图象可以得到乙队在第几分钟开始加速;
(3)根据函数图象可以去的甲乙对应的函数解析式,从而可以得到在什么时间范围内,甲队领先;
(4)根据函数图象可以求得相遇前,甲乙两队之间的距离不超过30m的时间范围.
解答 解:(1)由图象可得,
最先达到终点的是乙队,比甲队早到:(5-4.4)=0.6分钟,
故答案为:乙,0.6;
(2)由图象可得,
在比赛过程中,乙队在第1分钟和第3分钟时两次加速,
故答案为:1,3;
(3)设甲队对应的函数解析式为y=kx,
5k=800,得k=160,
即甲队对应的函数解析式为y=160x,
当3≤x≤4.4时,乙队对应的函数解析式为y=ax+b,
$\left\{\begin{array}{l}{3a+b=450}\\{4.4a+b=800}\end{array}\right.$,得$\left\{\begin{array}{l}{a=250}\\{b=-300}\end{array}\right.$,
即当3≤x≤4.4时,乙队对应的函数解析式为y=250x-300,
令250x-300<160x,得x<$\frac{10}{3}$,
即当0<x<$\frac{10}{3}$时,甲队领先;
(4)当0<x<1时,设乙对应的函数解析式为y=mx,
m=100,
即当0<x<1时,乙对应的函数解析式为y=100x,
160x-100x≤30,
解得,x≤0.5,
即当0<x≤0.5时,甲乙两队之间的距离不超过30m,
当1<x<3时,设乙队对应的函数解析式为y=cx+d,
$\left\{\begin{array}{l}{c+d=100}\\{3c+d=450}\end{array}\right.$,得$\left\{\begin{array}{l}{c=175}\\{d=-75}\end{array}\right.$,
当1<x<3时,乙队对应的函数解析式为y=175x-75,
160x-(175x-75)≤30,得x≥3(舍去),
乙在BC段对应的函数解析式为y=250x-300,
则160x-(250x-300)≤30,得x≥3,
令160x=250x-300,得x=$\frac{10}{3}$,
由上可得,当0<x≤0.5或3≤x≤$\frac{10}{3}$时,甲乙两队之间的距离不超过30m,
故答案为:0<x≤0.5或3≤x≤$\frac{10}{3}$.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,列出相应的函数解析式,利用数形结合的思想解答.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案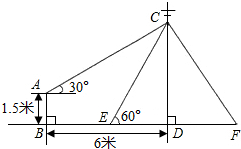 如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,则拉线CE的长为( )(结果保留小数点后一位,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73).
如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,则拉线CE的长为( )(结果保留小数点后一位,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73).| A. | 5.4 | B. | 5.7 | C. | 6.1 | D. | 6.3 |
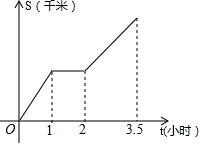 星期天,小明从家出发,以15千米/小时的速度骑车去郊游,到达目的地休息一段时间后原路返回,已知小明行驶的路程s(千米)与时间t(小时)之间的函数关系如图所示,则小明返程的速度为( )
星期天,小明从家出发,以15千米/小时的速度骑车去郊游,到达目的地休息一段时间后原路返回,已知小明行驶的路程s(千米)与时间t(小时)之间的函数关系如图所示,则小明返程的速度为( )| A. | 15千米/小时 | B. | 10千米/小时 | C. | 6千米/小时 | D. | 无法确定 |
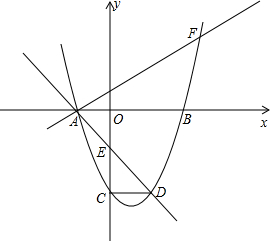 如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx-5与x轴交于A、B两点(点A在点B的左侧),与y轴交点为C,直线y=-x-2经过点A,交抛物线于点D,交y轴于点E,连接CD,并且∠ADC=45°.
如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx-5与x轴交于A、B两点(点A在点B的左侧),与y轴交点为C,直线y=-x-2经过点A,交抛物线于点D,交y轴于点E,连接CD,并且∠ADC=45°.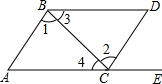 如图,点E在AC的延长线上,对于下列给出的四个条件:
如图,点E在AC的延长线上,对于下列给出的四个条件: 如图,AC⊥BC,AC=6,BC=8,AB=10,则点B到AC的距离为8.
如图,AC⊥BC,AC=6,BC=8,AB=10,则点B到AC的距离为8.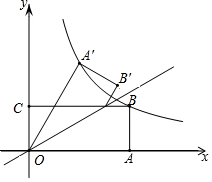 如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过点A′,B,则k的值为$\frac{4\sqrt{3}}{3}$.
如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过点A′,B,则k的值为$\frac{4\sqrt{3}}{3}$.