题目内容
9.y=x2,A、B两点在抛物线上,C为顶点,△ABC为正三角形,则S△ABC=3$\sqrt{3}$.分析 根据题意设B的坐标为(a,$\sqrt{3}$a),代入抛物线的解析式即可求得a的值,从而求得边长为2$\sqrt{3}$,CD=3,代入面积公式即可求得.
解答  解:如图,∵△ABC是等边三角形,
解:如图,∵△ABC是等边三角形,
∴设B(a,$\sqrt{3}$a),
代入y=x2得,$\sqrt{3}$a=a2,
解得a=$\sqrt{3}$,
∴AB=2$\sqrt{3}$,CD=3,
∴S△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$×$2\sqrt{3}$×3=3$\sqrt{3}$,
故答案为3$\sqrt{3}$.
点评 本题考查了等边三角形的性质和二次函数图象上点的坐标特征,根据题意设出B的坐标是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目

 如图,E是平行四边形ABCD边AD上一点,且AE:ED=1:2,CE与BD交于点O,则BO:OD=3:2.
如图,E是平行四边形ABCD边AD上一点,且AE:ED=1:2,CE与BD交于点O,则BO:OD=3:2.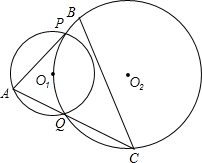 如图,⊙O1与⊙O2交于P、Q两点,且⊙O2经过点O1,A是⊙O1的优弧$\widehat{PQ}$上任一点,AP、AQ的延长线与⊙O2分别交于点B、C.证明:O1为△ABC的垂心.
如图,⊙O1与⊙O2交于P、Q两点,且⊙O2经过点O1,A是⊙O1的优弧$\widehat{PQ}$上任一点,AP、AQ的延长线与⊙O2分别交于点B、C.证明:O1为△ABC的垂心.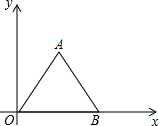 在平面直角坐标中.等边△OAB的OB在x轴上,0B=b,满足${a}^{2}-10a+25+\sqrt{b-4}=0$,D(a,0)
在平面直角坐标中.等边△OAB的OB在x轴上,0B=b,满足${a}^{2}-10a+25+\sqrt{b-4}=0$,D(a,0)