题目内容
如果方程x2+px+q=0的两个根是x1,x2,那么x1+x2=-p,x1•x2=q.请根据以上结论,解决下列问题:
(1)已知关于x的方程x2+mx+n=0(n≠0),求出一个一元二次方程,使它的两根分贝是已知方程两根的倒数;
(2)已知a、b满足a2-15a-5=0,b2-15b-5=0,求
+
的值;
(3)已知a、bc均为实数,且a+b+c=0,abc=16.
①求出一个含字母系数c的一元二次方程,使它的两根分别为a、b.
②求出整数c的最小值.
(1)已知关于x的方程x2+mx+n=0(n≠0),求出一个一元二次方程,使它的两根分贝是已知方程两根的倒数;
(2)已知a、b满足a2-15a-5=0,b2-15b-5=0,求
| a |
| b |
| b |
| a |
(3)已知a、bc均为实数,且a+b+c=0,abc=16.
①求出一个含字母系数c的一元二次方程,使它的两根分别为a、b.
②求出整数c的最小值.
考点:根与系数的关系
专题:计算题
分析:(1)设方程x2+mx+n=0(n≠0)的两根分别为a、b,根据根与系数的关系得到a+b=-m,ab=n,再计算出
+
=-
,
•
=
,然后根据根与系数的关系写出新方程;
(2)分类讨论:当a=b时,易得
+
═2;当a≠b时,则a、b可看作方程x2-15x-5=0的两实数根,根据根与系数的关系得到a+b=15,ab=-5,再利用完全平方根是变形得到
+
=
,然后利用整体代入的方法计算;
(3)①由于a+b+c=0,abc=16,则a+b=-c,ab=
,于是根据根与系数的关系可得两根分别为a、b的一元二次方程为x2+cx+
=0;
②利用根的判别式的意义得到△=c2-4×
≥0,解得c≥4,所以整数c的最小值为4.
| 1 |
| a |
| 1 |
| b |
| m |
| n |
| 1 |
| a |
| 1 |
| b |
| 1 |
| n |
(2)分类讨论:当a=b时,易得
| a |
| b |
| b |
| a |
| a |
| b |
| b |
| a |
| (a+b)2-2ab |
| ab |
(3)①由于a+b+c=0,abc=16,则a+b=-c,ab=
| 16 |
| c |
| 16 |
| c |
②利用根的判别式的意义得到△=c2-4×
| 16 |
| c |
解答:解:(1)设方程x2+mx+n=0(n≠0)的两根分别为a、b,
则a+b=-m,ab=n,
所以
+
=
=-
,
•
=
,
所以所求新方程为x2-(-
)+
=0,
整理得nx2+mx+1=0;
(2)当a=b时,
+
=1+1=2;
当a≠b时,a、b可看作方程x2-15x-5=0的两实数根,则a+b=15,ab=-5,
所以
+
=
=
=
=-47,
即
+
的值为2或-47;
(3)①∵a+b+c=0,abc=16,
∴a+b=-c,ab=
,
∴两根分别为a、b的一元二次方程可为x2+cx+
=0;
②∵△=c2-4×
≥0,
∴c3≥64,解得c≥4,
∴整数c的最小值为4.
则a+b=-m,ab=n,
所以
| 1 |
| a |
| 1 |
| b |
| a+b |
| ab |
| m |
| n |
| 1 |
| a |
| 1 |
| b |
| 1 |
| n |
所以所求新方程为x2-(-
| m |
| n |
| 1 |
| n |
整理得nx2+mx+1=0;
(2)当a=b时,
| a |
| b |
| b |
| a |
当a≠b时,a、b可看作方程x2-15x-5=0的两实数根,则a+b=15,ab=-5,
所以
| a |
| b |
| b |
| a |
| a2+b2 |
| ab |
| (a+b)2-2ab |
| ab |
| 152-2×(-5) |
| -5 |
即
| a |
| b |
| b |
| a |
(3)①∵a+b+c=0,abc=16,
∴a+b=-c,ab=
| 16 |
| c |
∴两根分别为a、b的一元二次方程可为x2+cx+
| 16 |
| c |
②∵△=c2-4×
| 16 |
| c |
∴c3≥64,解得c≥4,
∴整数c的最小值为4.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
在下列各组图形中,是全等的图形是( )
A、 |
B、 |
C、 |
D、 |
 如图所示,△ABC中,中线BD、CE相交于O,F、G分别为OB、OC的中点.判断四边形DEFG的形状并进行证明.
如图所示,△ABC中,中线BD、CE相交于O,F、G分别为OB、OC的中点.判断四边形DEFG的形状并进行证明.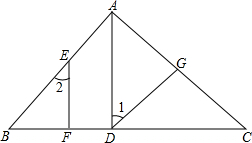 如图,在△ABC中,AD⊥BC于点D,EF⊥BC于点F,∠B=∠GDC,试说明∠1=∠2的理由.
如图,在△ABC中,AD⊥BC于点D,EF⊥BC于点F,∠B=∠GDC,试说明∠1=∠2的理由. 如图,已知
如图,已知