题目内容
12.关于x的方程:x+$\frac{1}{x}$=c+$\frac{1}{c}$的解为x1=c,x2=$\frac{1}{c}$;x-$\frac{1}{x}$=c-$\frac{1}{c}$(即x+$\frac{-1}{x}$=c+$\frac{-1}{c}$的解为x1=c,x2=-$\frac{1}{c}$;
x+$\frac{2}{x}$=c+$\frac{2}{c}$的解为x1=c,x2=$\frac{2}{c}$;x+$\frac{3}{x}$=c+$\frac{3}{c}$的解为x1=c,x2=$\frac{3}{c}$;…
(1)请观察上述方程与解的特征,比较关于x的方程x+$\frac{m}{c}$=c+$\frac{m}{c}$(m≠0)与它们的关系,猜想它的解是什么,并利用“方程的解”的概念进行验证;
(2)由上述的观察、比较、猜想、验证,可以得出结论:如果方程的左边是未知数与其倒数的和,方程右边的形式与左边完全相同,只有把其中的未知数换成某个常数,那么这样的方程可以直接得解.请用这个结论解关于x的方程:x+$\frac{2}{x-1}$=c+$\frac{2}{c-1}$.
分析 (1)根据已知方程的特点与解的关系即可写出方程的解;
(2)原方程可以变形为:x-1+$\frac{2}{x-1}$=c-1+$\frac{2}{c-1}$,把x-1当作一个整体,即可求解.
解答 解:(1)解是:x1=c,x2=$\frac{m}{c}$,
经检验:c和$\frac{m}{c}$是原方程的解;
(2)由x+$\frac{2}{x-1}$=c+$\frac{2}{c-1}$得x-1+$\frac{2}{x-1}$=c-1+$\frac{2}{c-1}$,
∴x-1=c-1,x-1=$\frac{2}{c-1}$,
∴x1=c,x2=$\frac{c+1}{c-2}$.
点评 本题主要考查了分式方程的解,解此题的关键是理解题意,认真审题,寻找规律.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
20.已知一次函数y1=k1x+b图象上的点A(t,m)和y2=k2x+b图象上的点B(t,n),且t>0,m<n,则k1与k2的大小关系是( )
| A. | k1<k2 | B. | k1=k2 | C. | k1>k2 | D. | 无法确定 |
17.点A(-4,a2+8)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.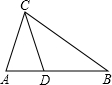 如图,下列四个条件:
如图,下列四个条件:
①AC:CD=AB:BC且∠ACD=∠B;②CD:AD=BC:AC;③AC2=AD•AB;④CD2=AD•DB
能保证使△ACD与△ABC相似的个数是( )
 如图,下列四个条件:
如图,下列四个条件:①AC:CD=AB:BC且∠ACD=∠B;②CD:AD=BC:AC;③AC2=AD•AB;④CD2=AD•DB
能保证使△ACD与△ABC相似的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
1.一辆汽车在广阔的草原上行驶,两次拐弯后,行驶的方向与原来的方向相同,那么这两次拐弯的角度可能是( )
| A. | 第一次向右拐40°,第二次向右拐140° | |
| B. | 第一次向右拐40°,第二次向左拐40° | |
| C. | 第一次向左拐40°,第二次向右拐140° | |
| D. | 第一次向右拐140°,第二次向左拐40° |
 如图,已知点A从点(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O、A为顶点作菱形OABC,使点B、C在第一象限内,且∠AOC=60°,点P的坐标为(0,3),设点A运动了t秒,求:
如图,已知点A从点(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O、A为顶点作菱形OABC,使点B、C在第一象限内,且∠AOC=60°,点P的坐标为(0,3),设点A运动了t秒,求: 边长为a的菱形是由边长为a的正方形“形变”得到的,若这个菱形一组对边之间的距离为h,则称$\frac{a}{h}$为这个菱形的“形变度”.
边长为a的菱形是由边长为a的正方形“形变”得到的,若这个菱形一组对边之间的距离为h,则称$\frac{a}{h}$为这个菱形的“形变度”.