题目内容
4.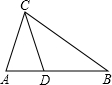 如图,下列四个条件:
如图,下列四个条件:①AC:CD=AB:BC且∠ACD=∠B;②CD:AD=BC:AC;③AC2=AD•AB;④CD2=AD•DB
能保证使△ACD与△ABC相似的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据有两组角对应相等的两个三角形相似对①进行判断;根据两组对应边的比相等且夹角对应相等的两个三角形相似对②③④进行判断.
解答 解:∵∠ACD=∠B,
而∠CAD=∠BAC,
∴△ACD∽△ABC,所以①正确;
∵CD:AD=BC:AC,
∴$\frac{AC}{AB}$=$\frac{BC}{CD}$,
∴∠CAD=∠BAC,
∴不能判断△ACD与△ABC相似,所以②错误;
∵AC2=AD•AB,即AC:AD=AB:AC,
而∠CAD=∠BAC,
∴△ACD∽△ABC,所以③正确;
∵CD2=AD•DB,即CD:AD=DB:CD,
而∠CAD=∠BAC,
∴不能判断△ACD与△ABC相似,所以④错误.
故选C.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.必然事件的概率是( )
| A. | 0 | B. | 0.5 | C. | 1 | D. | 不能确定 |
 用
用 表示三种不同的物体,现放在天平上比较两次,情况如图所示,那么,这三种物体质量的大小关系应为a=b<c.
表示三种不同的物体,现放在天平上比较两次,情况如图所示,那么,这三种物体质量的大小关系应为a=b<c.