题目内容
3. 如图,已知点A从点(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O、A为顶点作菱形OABC,使点B、C在第一象限内,且∠AOC=60°,点P的坐标为(0,3),设点A运动了t秒,求:
如图,已知点A从点(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O、A为顶点作菱形OABC,使点B、C在第一象限内,且∠AOC=60°,点P的坐标为(0,3),设点A运动了t秒,求:(1)点C的坐标(用含t的代数式表示);
(2)点A在运动过程中,当t为何值时,使得△OCP为等腰三角形?
分析 (1)过点C作CH⊥x轴于点H,解直角三角形CHO,求出OH,CH的长,即可求出点C的坐标;
(2)因为等腰三角形OCP的腰和底不确定所以要分三种情况分别讨论:①当以O为等腰三角形顶点时;②当以C为等腰三角形顶点时;③当以P为等腰三角形顶点时,求出t的值即可.
解答 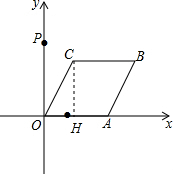 解:(1)过点C作CH⊥x轴于点H,
解:(1)过点C作CH⊥x轴于点H,
根据题意得:OA=1+t,
∵四边形OABC是菱形,
∴OC=OA=1+t,
∵∠AOC=60°,
∴OH=OC•cos60°=$\frac{1}{2}$OC=$\frac{1}{2}$(1+t),CH=OC•sin60°=$\frac{\sqrt{3}}{2}$(1+t),
∴点C的坐标为:($\frac{1}{2}$(1+t),$\frac{\sqrt{3}}{2}$(1+t));
(2)①当以O为等腰三角形顶点时,OC=OP,
∴1+t=3,
∴t=2;
②当以C为等腰三角形顶点时,PC=OC,则CH=$\frac{1}{2}$OP=$\frac{3}{2}$,
即$\frac{\sqrt{3}}{2}$(1+t)=$\frac{3}{2}$,
解得:t=$\sqrt{3}$-1;
③当以P为等腰三角形顶点时,OP=PC,∠POC=30°,
∴OC=3$\sqrt{3}$,
∴1+t=3$\sqrt{3}$,
∴t=3$\sqrt{3}$-1,
综上可知,当t=$\sqrt{3}$-1,t=2,t=3$\sqrt{3}$-1时,均可使得△OCP为等腰三角形.
点评 此题考查了菱形的性质,特殊角的三角函数值以及等腰三角形的判定和性质,解题的关键是充分利用了分类讨论的思想以保证做题时做到不重不漏.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8. 如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC的大小是( )
如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC的大小是( )
 如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC的大小是( )
如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC的大小是( )| A. | 105° | B. | 110° | C. | 100° | D. | 120° |
13.必然事件的概率是( )
| A. | 0 | B. | 0.5 | C. | 1 | D. | 不能确定 |