题目内容
5. 如图,已知△ABC和△ADC均为直角三角形,点B,D位于AC的两侧,∠ACB=∠ADC=90°,BC=a,AC=b,AB=c,要使△ACD∽△ABC,CD可以等于( )
如图,已知△ABC和△ADC均为直角三角形,点B,D位于AC的两侧,∠ACB=∠ADC=90°,BC=a,AC=b,AB=c,要使△ACD∽△ABC,CD可以等于( )| A. | $\frac{{a}^{2}}{c}$ | B. | $\frac{{b}^{2}}{a}$ | C. | $\frac{ab}{c}$ | D. | $\frac{{b}^{2}}{ac}$ |
分析 直接利用相似三角形的性质得出$\frac{DC}{BC}$=$\frac{AC}{AB}$,进而得出答案.
解答 解:∵△ACD∽△ABC,
∴$\frac{DC}{BC}$=$\frac{AC}{AB}$,
∵BC=a,AC=b,AB=c,
∴$\frac{DC}{a}$=$\frac{b}{c}$,
则DC=$\frac{ab}{c}$.
故选:C.
点评 此题主要考查了相似三角形判定与性质,正确得出比例式是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列语句正确的是( )
| A. | $\sqrt{64}$的立方根是4 | B. | -3的立方根是27 | ||
| C. | $\frac{8}{27}$的立方根是±$\frac{2}{3}$ | D. | 立方根等于本身的数是-1、0、1 |
10.下列说法正确的是( )
| A. | $\sqrt{81}$的平方根是±9 | B. | $\sqrt{64}$的立方根是±2 | ||
| C. | x为任意数都有$\root{3}{{x}^{3}}$=x | D. | 16的平方根是4 |
20.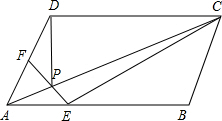 已知平行四边形ABCD中,E,F分别是AB,AD上的点,EF与对角线AC交于P,若$\frac{AE}{EB}$=$\frac{1}{2}$,$\frac{AF}{FD}$=$\frac{2}{3}$,则$\frac{{S}_{△PAD}}{{S}_{△PCE}}$的值为( )
已知平行四边形ABCD中,E,F分别是AB,AD上的点,EF与对角线AC交于P,若$\frac{AE}{EB}$=$\frac{1}{2}$,$\frac{AF}{FD}$=$\frac{2}{3}$,则$\frac{{S}_{△PAD}}{{S}_{△PCE}}$的值为( )
 已知平行四边形ABCD中,E,F分别是AB,AD上的点,EF与对角线AC交于P,若$\frac{AE}{EB}$=$\frac{1}{2}$,$\frac{AF}{FD}$=$\frac{2}{3}$,则$\frac{{S}_{△PAD}}{{S}_{△PCE}}$的值为( )
已知平行四边形ABCD中,E,F分别是AB,AD上的点,EF与对角线AC交于P,若$\frac{AE}{EB}$=$\frac{1}{2}$,$\frac{AF}{FD}$=$\frac{2}{3}$,则$\frac{{S}_{△PAD}}{{S}_{△PCE}}$的值为( )| A. | $\frac{3}{7}$ | B. | $\frac{2}{3}$ | C. | $\frac{18}{13}$ | D. | $\frac{18}{7}$ |