题目内容
 济南大学举行的一场排球赛中,队员黄娟站在边线发球,发球点与地面的距离为1.8米,发球的方向与边线垂直,球飞行的路线为抛物线,当球飞行距离为8米时,达到最高高度为5.2米,已知球场的长18米,请计算球是否落到球场的对方边界线外?
济南大学举行的一场排球赛中,队员黄娟站在边线发球,发球点与地面的距离为1.8米,发球的方向与边线垂直,球飞行的路线为抛物线,当球飞行距离为8米时,达到最高高度为5.2米,已知球场的长18米,请计算球是否落到球场的对方边界线外?考点:二次函数的应用
专题:
分析:首先利用顶点式求出抛物线解析式,进而利用y=0时求出图象与x轴交点横坐标,即可得出答案.
解答:解:由题意得:
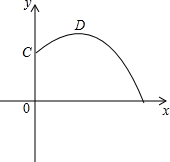
C点为发球点,D点为最高点.球运行的轨迹是抛物线,因为其顶点为(8,5.2)
所以设y=a(x-8)2+5.2,再由发球点坐标(0,1.8)代入得:
y=a(x-8)2+5.2,
a=-
,
所以解析式为:y=-
(x-8)2+5.2,
令y=0,
解得:x≈18.89>18.
所以球落到球场的对方边界线外.
C点为发球点,D点为最高点.球运行的轨迹是抛物线,因为其顶点为(8,5.2)
所以设y=a(x-8)2+5.2,再由发球点坐标(0,1.8)代入得:
y=a(x-8)2+5.2,
a=-
| 17 |
| 320 |
所以解析式为:y=-
| 17 |
| 320 |
令y=0,
解得:x≈18.89>18.
所以球落到球场的对方边界线外.
点评:此题主要考查了二次函数的应用以及顶点式求二次函数解析式,利用数形结合得出抛物线解析式是解题关键.

练习册系列答案
相关题目
