题目内容
在本学期期末复习中,我们已遇到了这样的问题:已知
=
,
=
,
=
,求
的值.根据条件中式子的特点,我们可能会想起
+
=
,于是将每一个分式的分子、分母颠倒位置,问题被转化为“已知
+
=2,
+
=3,
+
=4,求
+
+
的值”,这样解答就方便了.
(1)通过阅读,上文中原问题
= ;
(2)类比文中的处理方法与思路,求解下列问题:已知:
=
,求
的值.
| ab |
| a+b |
| 1 |
| 2 |
| bc |
| b+c |
| 1 |
| 3 |
| ca |
| a+c |
| 1 |
| 4 |
| abc |
| ab+bc+ca |
| 1 |
| a |
| 1 |
| b |
| a+b |
| ab |
| 1 |
| a |
| 1 |
| b |
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
| 1 |
| c |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
(1)通过阅读,上文中原问题
| abc |
| ab+bc+ca |
(2)类比文中的处理方法与思路,求解下列问题:已知:
| m |
| m2+1 |
| 1 |
| 5 |
| 8m2 |
| m4+m2+1 |
考点:分式的化简求值
专题:阅读型
分析:(1)原式分子分母除以abc变形后,将已知等式代入计算即可求出值;
(2)已知等式变形求出m+
的值,原式变形后代入计算即可求出值.
(2)已知等式变形求出m+
| 1 |
| m |
解答:解:(1)∵
+
=2,
+
=3,
+
=4,
∴原式=
=
;
故答案为:
;
(2)已知等式变形得:
=
,得到m+
=5,
则原式=
=
=
=
.
| 1 |
| a |
| 1 |
| b |
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
| 1 |
| c |
∴原式=
| 1 | ||||||
|
| 1 |
| 9 |
故答案为:
| 1 |
| 9 |
(2)已知等式变形得:
| 1 | ||
m+
|
| 1 |
| 5 |
| 1 |
| m |
则原式=
| 8 | ||
m2+
|
| 8 | ||
(m+
|
| 8 |
| 25-1 |
| 1 |
| 3 |
点评:此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
下列图形中是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
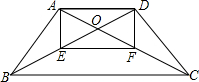 如图,在梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD交于点O,E、F分别为OB、OC的中点.
如图,在梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD交于点O,E、F分别为OB、OC的中点.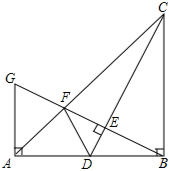 如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①
如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①