题目内容
7.计算(1)$\frac{2}{\sqrt{2}}$-($\sqrt{2}$)2+(π+$\sqrt{2}$)0-$\sqrt{8}$+|$\sqrt{2}$-1|;
(2)($\sqrt{3}$+$\sqrt{2}$)2-($\sqrt{3}$+$\sqrt{2}$)($\sqrt{3}$-$\sqrt{2}$).
分析 (1)根据零指数幂的意义和绝对值的意义得到原式=$\sqrt{2}$-2+1-2$\sqrt{2}$+$\sqrt{2}$-1,然后合并即可;
(2)利用完全平方公式和平方差公式计算.
解答 解:(1)原式=$\sqrt{2}$-2+1-2$\sqrt{2}$+$\sqrt{2}$-1
=-2;
(2)原式=3+2$\sqrt{6}$+2-(3-2)
=5+2$\sqrt{6}$-1
=4+2$\sqrt{6}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
16.已知某种儿童米粉的标准质量为200g,苏果超市从购进的儿童米粉中随机抽取8袋检测每袋的质量是否符合标准质量,超过与不足的质量分别用正、负数表示,例如+2表示该袋米粉超过标准质量2g,现记录如表:
(1)指出编号为几的米粉最接近标准质量?
(2)在抽取的八袋米粉中最重的那袋比最轻的那袋多多少克?
(3)这次抽样的八袋米粉的总质量是多少?
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 偏差 | +1 | -2 | -1 | -2 | -0.5 | +4 | +2 | -1 |
(2)在抽取的八袋米粉中最重的那袋比最轻的那袋多多少克?
(3)这次抽样的八袋米粉的总质量是多少?
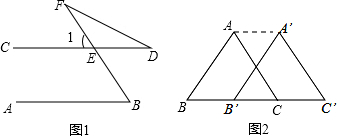
 如图,已知AB是⊙O的直径,点C、D在⊙O上,且AB=5,BC=3.
如图,已知AB是⊙O的直径,点C、D在⊙O上,且AB=5,BC=3.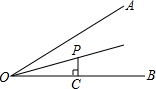 如图,∠AOB=30°,OP平分∠AOB,PC⊥OB于点C,若OC=1,则PC的长是2-$\sqrt{3}$.
如图,∠AOB=30°,OP平分∠AOB,PC⊥OB于点C,若OC=1,则PC的长是2-$\sqrt{3}$.