题目内容
2. 如图,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m.
如图,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m.(1)建立如图所示的坐标系,求抛物线的解析式;
(2)一艘装满物资的小船,露出水面部分的高为0.8m、宽为4m(横断面如图所示).若暴雨后,水位达到警戒线CD,此时这艘船能从这座拱桥下通过吗?请说明理由.
分析 (1)先设抛物线的解析式y=ax2,再找出几个点的坐标,代入解析式后可求解.
(2)求出拱桥顶O到CD的距离为1m,x=2时,y=-0.16,由此即可判定.
解答 解:(1)设所求抛物线的解析式为:y=ax2(a≠0),
由CD=10m,可设D(5,b),
由AB=20m,水位上升3m就达到警戒线CD,
则B(10,b-3),
把D、B的坐标分别代入y=ax2得:
$\left\{\begin{array}{l}{25a=b}\\{100a=b-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{1}{25}}\\{b=-1}\end{array}\right.$.
∴y=-$\frac{1}{25}$x2;
(2))∵b=-1,
∴拱桥顶O到CD的距离为1m,
∵x=2时,y=-$\frac{4}{25}$=-0.16,
1-0.8=0.2>0.16,
∴水位达到警戒线CD,此时这艘船能从这座拱桥下通过.
点评 本题考查二次函数的应用,解题的关键是把一个实际问题通过数学建模,转化为二次函数问题,用二次函数的性质加以解决.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
14.2016年广安国际红色马拉松赛吸引约168000人次观赛.将168000用科学记数法表示正确的是( )
| A. | 168×103 | B. | 16.8×104 | C. | 1.68×105 | D. | 0.168×106 |
12.下列说法中正确的是( )
| A. | 近似数0.66有两个有效数字 | B. | 近似数5.01×103精确到百分位 | ||
| C. | 近似数2.10精确到十分位 | D. | 近似数5.8万精确到万位 |
 已知线段a、b以及∠α,求作△ABC,使得AB+AC=a,且BC=b,∠A=∠α.
已知线段a、b以及∠α,求作△ABC,使得AB+AC=a,且BC=b,∠A=∠α.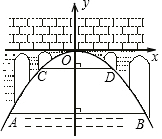 有一座抛物线形拱桥,校下面在正常水位时AB宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米.
有一座抛物线形拱桥,校下面在正常水位时AB宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米.