题目内容
如图，△ABC中，D是BC的中点，AB=4| 3 |
| 3 |
考点：勾股定理
专题：
分析：作辅助线构建平行四边形ABEC，然后根据平行四边形的对边平行且相等及勾股定理的逆定理解答即可．
解答：
解：延长AD到E，使DE=AD=3，连接BE，CE．
∵D是BC的中点，
∴CD=BD，
∴四边形ABEC是平行四边形，
∴AB∥CE，EB=CA=2
，
∵62+（2
）2=（4
）2，即AE2+AC2=EC2，
∴∠EAC=90°，
∴∠EAB=90°，
∴CD=
=
=
，
∴BC=2CD=2
，
∴S△ABC=2S△ACD=2×
AC•AD=2
×3=6
．
综上所述，BC的长度为2
，△ABC的面积是6
．
解：延长AD到E，使DE=AD=3，连接BE，CE．∵D是BC的中点，
∴CD=BD，
∴四边形ABEC是平行四边形，
∴AB∥CE，EB=CA=2
| 3 |
∵62+（2
| 3 |
| 3 |
∴∠EAC=90°，
∴∠EAB=90°，
∴CD=
| AD2+AC2 |
32+(2
|
| 21 |
∴BC=2CD=2
| 21 |
∴S△ABC=2S△ACD=2×
| 1 |
| 2 |
| 3 |
| 3 |
综上所述，BC的长度为2
| 21 |
| 3 |
点评：本题考查勾股定理的逆定理的应用、平行四边形的判定与性质．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．
练习册系列答案
阅读快车系列答案
相关题目
如图，∵∠B=∠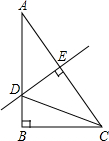
如图．在Rt△ABC中，∠A=30°，DE垂直平分斜边AC，交AB于D，E式垂足，连接CD，若BD=1，则AD的长是（ ）