题目内容
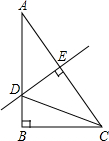 如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E式垂足,连接CD,若BD=1,则AD的长是( )
如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E式垂足,连接CD,若BD=1,则AD的长是( )A、
| ||
| B、2 | ||
| C、4 | ||
| D、1 |
考点:线段垂直平分线的性质,含30度角的直角三角形
专题:
分析:先根据三角形内角和定理求出∠ACB,根据线段垂直平分线求出AD=CD,求出∠ACD、∠DCB,由直角三角形的性质可得出CD的长.
解答:解:∵∠A=30°,∠B=90°,
∴∠ACB=180°-30°-90°=60°,
∵DE垂直平分斜边AC,
∴AD=CD,
∴∠A=∠ACD=30°,
∴∠DCB=60°-30°=30°,
∵BD=1,
∴CD=AD=2.
故选B.
∴∠ACB=180°-30°-90°=60°,
∵DE垂直平分斜边AC,
∴AD=CD,
∴∠A=∠ACD=30°,
∴∠DCB=60°-30°=30°,
∵BD=1,
∴CD=AD=2.
故选B.
点评:本题考查的是线段垂直平分线的性质,含30度角的直角三角形,等腰三角形的性质,三角形的内角和定理等知识点的应用,主要考查学生运用这些定理进行推理的能力,题目综合性比较强,难度适中.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
下列语句中正确的是( )
| A、0没有相反数和绝对值 |
| B、没有绝对值最小的有理数 |
| C、有理数包括整数和分数 |
| D、互为相反数的两个数的和不一定为零 |
下列去括号正确的是( )
| A、-(2x-5)=-2x+5 | ||||
B、-
| ||||
C、
| ||||
D、-(
|
 实验发现:光线从空气射入玻璃中,会发生折射现象,光线从玻璃射入空气中,同样也会发生折射现象.如图,光线从空气中射入玻璃中再从玻璃射入空气中,已知∠1=∠2,∠3=∠4,那么光线AB与CD是否平行?说明理由.
实验发现:光线从空气射入玻璃中,会发生折射现象,光线从玻璃射入空气中,同样也会发生折射现象.如图,光线从空气中射入玻璃中再从玻璃射入空气中,已知∠1=∠2,∠3=∠4,那么光线AB与CD是否平行?说明理由. 如图,△ABC中,D是BC的中点,AB=
如图,△ABC中,D是BC的中点,AB= 如图所示,在数轴上A点表示数a,B点表示数b,且a、b满足|2a+6|+|b-9|=0(1)点A表示的数为
如图所示,在数轴上A点表示数a,B点表示数b,且a、b满足|2a+6|+|b-9|=0(1)点A表示的数为