题目内容
13.当a、b为何值时,多项式a2-2ab+2b2-2a-4b+27有最小值,并求出这个最小值.分析 利用配方法将多项式a2-2ab+2b2-2a-4b+27转化为(a-b-1)2+(b-3)2+17,然后利用非负数的性质进行解答.
解答 解:∵a2-2ab+2b2-2a-4b+27
=a2-2a(b+1)+(b+1)2+(b-3)2+17
=(a-b-1)2+(b-3)2+17,
∴当a=4,b=3时,多项式a2-2ab+2b2-2a-4b+27有最小值17.
点评 此题考查了配方法的应用,以及非负数的性质,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.一个数的倒数是它的本身,这个数是( )
| A. | 0 | B. | 1 | C. | -1 | D. | 1或-1 |
8.$\frac{2}{5}:4$化为最简整数比是( )
| A. | 1:10 | B. | 8:5 | C. | 10:1 | D. | 5:8 |
18.若|a|=5,|b|=7且|a+b|=a+b,则a-b的值为( )
| A. | 2或-2 | B. | 12或-12 | C. | -2或-12 | D. | 5或7 |
5. 如图是婴儿车的平面示意图,其中AB∥CD,∠1=124°,∠3=40°,那么∠2的度数为( )
如图是婴儿车的平面示意图,其中AB∥CD,∠1=124°,∠3=40°,那么∠2的度数为( )
 如图是婴儿车的平面示意图,其中AB∥CD,∠1=124°,∠3=40°,那么∠2的度数为( )
如图是婴儿车的平面示意图,其中AB∥CD,∠1=124°,∠3=40°,那么∠2的度数为( )| A. | 74° | B. | 76° | C. | 84° | D. | 86° |
3.将有理数$\frac{85}{84}$,$\frac{88}{87}$,$\frac{84}{83}$,$\frac{87}{86}$,$\frac{86}{85}$两两相乘得到10个积,将10个积从大到小顺序排列,排在第5个的积是有理数( )的乘积.
| A. | $\frac{84}{83}$和$\frac{88}{87}$ | B. | $\frac{86}{85}$和$\frac{88}{87}$ | C. | $\frac{85}{84}$和$\frac{87}{86}$ | D. | $\frac{86}{85}$和$\frac{87}{86}$ |
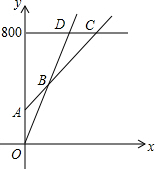 某市游泳馆为了满足不同顾客的需求,设计了三种游泳票:普通票价每次20元/张;金卡售价800元/张,每次凭卡不再收费;银卡售价200元/张,每次凭卡另收10元.这样顾客可根据游泳次数的多少选择不同的消费方式.普通票全年正常出售,两种优惠卡仅限暑期使用,不限次数.设游泳x次时,所需总费用为y元.
某市游泳馆为了满足不同顾客的需求,设计了三种游泳票:普通票价每次20元/张;金卡售价800元/张,每次凭卡不再收费;银卡售价200元/张,每次凭卡另收10元.这样顾客可根据游泳次数的多少选择不同的消费方式.普通票全年正常出售,两种优惠卡仅限暑期使用,不限次数.设游泳x次时,所需总费用为y元.