题目内容
7.已知关于x的一元二次方程x2-6x+2m+1=0有实数根.(1)求实数m的取值范围;
(2)若方程的两个实数根为x1,x2,且x1x2+x1+x2=15,求m的值.
分析 (1)由根的判别式△≥0来求实数m的取值范围;
(2)直接利用根与系数的关系解答.
解答 解:(1)由题意得,△=(-6)2-4(2m+1)≥0,
解得m≥4;
(2)∵关于x的一元二次方程x2-6x+2m+1=0的两个实数根为x1,x2,
∴x1x2=2m+1,x1+x2=6,
∴x1x2+x1+x2=2m+1+6=15,
解得m=4.
点评 本题考查了根与系数的关系,根的判别式.
总结:一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
相关题目
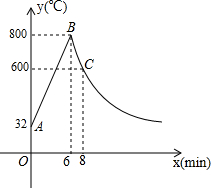 如图,制作某金属工具先将材料煅烧6分钟温度升到800℃,再停止煅烧进行锻造,8分钟温度降为600℃;煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时温度y(℃)与时间x(min)成反比例函数关系;该材料初始温度是32℃.
如图,制作某金属工具先将材料煅烧6分钟温度升到800℃,再停止煅烧进行锻造,8分钟温度降为600℃;煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时温度y(℃)与时间x(min)成反比例函数关系;该材料初始温度是32℃.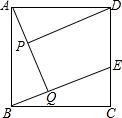 已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.求证:AP=BQ.
已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.求证:AP=BQ.
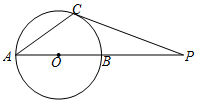 如图,点C在⊙O上,过点C作⊙O的切线,与直径AB的延长线交于点P,连接AC,若∠A=35°,则∠P=20度.
如图,点C在⊙O上,过点C作⊙O的切线,与直径AB的延长线交于点P,连接AC,若∠A=35°,则∠P=20度.