题目内容
19.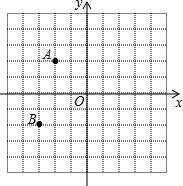 如图,在平面直角坐标系中,A(-2,2),B(-3,-2).
如图,在平面直角坐标系中,A(-2,2),B(-3,-2).(1)①若点C与点A关于原点O对称,则点C的坐标为(2,-2);②将点A向右平移5个单位得到点D,则点D的坐标为(3,2);
(2)在由点A,B,C,D组成的四边形ABCD内(不包括边界)任取一个横、纵坐标均为整数的点,求所取的点恰好落在双曲线$y=\frac{2}{x}$的概率.
分析 (1)①根据两个点关于原点对称时,它们的坐标符号相反确定C点坐标;②根据点的平移方法可得A点横坐标加5,纵坐标不变可得D点位置;
(2)顺次连接A、B、C、D,可得四边形ABCD,找出范围内的横、纵坐标均为整数的点的个数,再根据反比例函数图象上点的坐标特点可得横纵坐标之积为2且在由点A,B,C,D组成的四边形ABCD内的有(2,1)(-2,-1),再利用概率公式可得答案.
解答  解:(1)①∵A(-2,2),
解:(1)①∵A(-2,2),
∴与点A关于原点O对称的C点坐标(2,-2);
故答案为:(2,-2);
②将点A向右平移5个单位得到点D,则点D的坐标为(-2+5,2),
即(3,2),
故答案为:(3,2);
(2)恰好落在双曲线$y=\frac{2}{x}$的点横纵坐标之积为2,
横、纵坐标均为整数的点共有15个,
横纵坐标之积为2且在由点A,B,C,D组成的四边形ABCD内的有(2,1)(-2,-1),共2个,
概率为$\frac{2}{15}$.
点评 此题主要考查了反比例函数图象上点的坐标特点,以及关于原点对称的点的坐标特点,点的平移,概率公式,关键是熟练掌握课本基础知识.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
7.若⊙O的直径为10cm,点A到圆心O的距离为4cm,那么点A与⊙O的位置关系是( )
| A. | 点A在圆外 | B. | 点A在圆上 | C. | 点A在圆内 | D. | 不能确定 |
14. 已知△ABC在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则点P叫做△ABC的( )
已知△ABC在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则点P叫做△ABC的( )
 已知△ABC在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则点P叫做△ABC的( )
已知△ABC在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则点P叫做△ABC的( )| A. | 外心 | B. | 内心 | C. | 重心 | D. | 无法确定 |
8.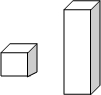 图中的两个长方体底面相同而高度不同,关于这两个长方体的视图说法正确的是( )
图中的两个长方体底面相同而高度不同,关于这两个长方体的视图说法正确的是( )
 图中的两个长方体底面相同而高度不同,关于这两个长方体的视图说法正确的是( )
图中的两个长方体底面相同而高度不同,关于这两个长方体的视图说法正确的是( )| A. | 主视图相同 | B. | 俯视图相同 | ||
| C. | 左视图相同 | D. | 主视图、俯视图、左视图都相同 |
 己知如图,在直角坐标系中,矩形ABCD,点A(3,6),点B(5,6),点C(5,10),直线l:y=x以每秒1个单位的速度沿y轴向上运动,运动的时间为t秒.试解决下列问题:
己知如图,在直角坐标系中,矩形ABCD,点A(3,6),点B(5,6),点C(5,10),直线l:y=x以每秒1个单位的速度沿y轴向上运动,运动的时间为t秒.试解决下列问题: