题目内容
11．点（2，4）关于y轴的对称点的坐标是（-2，4）．分析 利用关于y轴对称点的坐标特点：横坐标互为相反数，纵坐标不变．即点P（x，y）关于y轴的对称点P′的坐标是（-x，y），进而得出答案．
解答 解：点（2，4）关于y轴的对称点的坐标是：（-2，4）．
故答案为：（-2，4）．
点评 此题主要考查了关于y轴对称点的性质，正确把握横纵坐标关系是解题关键．
练习册系列答案
相关题目
2．-$\frac{1}{2003}$的倒数为（ ）
| A． | $\frac{1}{2003}$ | B． | -$\frac{1}{2003}$ | C． | 2013 | D． | -2013 |
19．下列实数中是无理数的是（ ）
| A． | $\sqrt{4}$ | B． | π | C． | 0.$\stackrel{•}{3}$$\stackrel{•}{8}$ | D． | -$\frac{22}{7}$ |
如图，⊙O是△ABC的外接圆，∠ABC=45°，延长BC于D，连接AD，使得AD∥OC，AB交OC于E．
16．某地要把248吨物资从某地运往甲、乙两地，用大、小两种货车共20辆，恰好能一次性运完这批物资．已知这两种货车的载重量分别为16吨/辆和10吨/辆，运往甲、乙两地的运费如下表：
（1）求这两种货车各用多少辆？
（2）如果安排9辆货车前往甲地，其余货车前往乙地，设前往甲地的大货车为a辆，前往甲、乙两地的总运费为w元，求出w与a的函数关系式（写出自变量的取值范围）．
（3）在（2）的条件下，若运往甲地的物资不少于120吨，请你设计出使总运费最少的货车调配方案，并求出最少总运费．
| 运往地车型 | 甲地（元/辆） | 乙地（元/辆） |
| 大货车 | 620 | 700 |
| 小货车 | 400 | 550 |
（2）如果安排9辆货车前往甲地，其余货车前往乙地，设前往甲地的大货车为a辆，前往甲、乙两地的总运费为w元，求出w与a的函数关系式（写出自变量的取值范围）．
（3）在（2）的条件下，若运往甲地的物资不少于120吨，请你设计出使总运费最少的货车调配方案，并求出最少总运费．
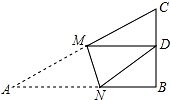如图，Rt△ABC中，AB=6，BC=4，∠B=90°，将△ABC折叠，使点A与BC的中点D重合，折痕为MN，则线段BN的长为$\frac{8}{3}$．