题目内容
10.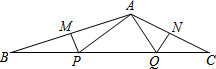 如图,∠BAC=130°,若MP和QN分别垂直平分AB和AC,则∠PAQ等于80°.
如图,∠BAC=130°,若MP和QN分别垂直平分AB和AC,则∠PAQ等于80°.
分析 由MP和QN分别垂直平分AB和AC,根据线段垂直平分线的性质,可得PA=PB,QA=QC,继而可得∠BAP+∠CAQ=∠B+∠C=180°-∠BAC=50°,则可求得答案.
解答 解:∵MP和QN分别垂直平分AB和AC,
∴PA=PB,QA=QC,
∴∠BAP=∠B,∠CAQ=∠C,
∵∠BAC=130°,
∴∠BAP+∠CAQ=∠B+∠C=180°-∠BAC=50°,
∴∠PAQ=∠BAC-(∠BAP+∠CAQ)=80°.
故答案为:80°.
点评 此题考查了线段垂直平分线的性质以及等腰三角形的性质.注意转化思想的应用是关键.

练习册系列答案
相关题目
15.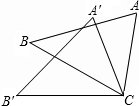 如图,△ACB≌△A′CB′,∠A′CB′=65°,∠A′CB=35°,则∠ACA′的度数( )
如图,△ACB≌△A′CB′,∠A′CB′=65°,∠A′CB=35°,则∠ACA′的度数( )
 如图,△ACB≌△A′CB′,∠A′CB′=65°,∠A′CB=35°,则∠ACA′的度数( )
如图,△ACB≌△A′CB′,∠A′CB′=65°,∠A′CB=35°,则∠ACA′的度数( )| A. | 20° | B. | 30° | C. | 35° | D. | 40° |
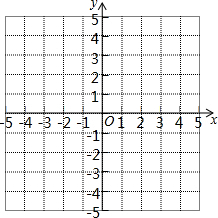 利用图象解方程组$\left\{\begin{array}{l}{2x+y=0}\\{x-y=6}\end{array}\right.$.
利用图象解方程组$\left\{\begin{array}{l}{2x+y=0}\\{x-y=6}\end{array}\right.$.
 已知:如图,E是等腰三角形ABC的腰AC上的任意一点,ED⊥BC,垂足为D,延长DE交BA的延长线于点F.求证:点A在EF的垂直平分线上.
已知:如图,E是等腰三角形ABC的腰AC上的任意一点,ED⊥BC,垂足为D,延长DE交BA的延长线于点F.求证:点A在EF的垂直平分线上.