题目内容
有一根直尺短边长2厘米,长边长10厘米,还有一块锐角为45°的直角三角形纸板,它的斜边长为12厘米.如图甲,将直尺的短边DE与直角三角形纸板的斜边AB重合,且点D与点A重合.将直尺沿射线AB方向平移,如图乙,设平移的长度为xcm,且满足0≤x≤10,直尺和三角形纸板重叠部分的面积(即图中阴影部分)为Scm2.
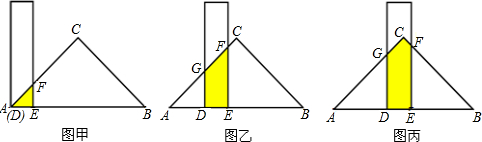
(1)当x=0cm时,S= ;当x=4cm时,S= ;当x=10cm时,S= .
(2)当4<x<6时(如图丙),请用含x的代数式表示S.
(3)是否存在一个位置,使阴影部分面积为11cm2?若存在,请求出此时x的值.

(1)当x=0cm时,S=
(2)当4<x<6时(如图丙),请用含x的代数式表示S.
(3)是否存在一个位置,使阴影部分面积为11cm2?若存在,请求出此时x的值.
考点:相似形综合题
专题:
分析:(1)当x=0cm时,直尺和三角形纸板重叠部分的面积是两直角边都为2厘米的三角形面积;当x=4cm时,直尺和三角形纸板重叠部分的面积=两直角边都为6厘米的三角形面积-两直角边都为4厘米的三角形面积;当x=10cm时,直尺和三角形纸板重叠部分的面积是两直角边都为2厘米的三角形面积;
(2)过点C做CM⊥AB于点M.当4<x<6时,根据S=梯形GDMC的面积+梯形CMEF的面积,列式计算即可求解;
(3)根据阴影部分面积为11cm2,列出方程-x2+10x-14=11,解方程即可求解.
(2)过点C做CM⊥AB于点M.当4<x<6时,根据S=梯形GDMC的面积+梯形CMEF的面积,列式计算即可求解;
(3)根据阴影部分面积为11cm2,列出方程-x2+10x-14=11,解方程即可求解.
解答:解:(1)当x=0cm时,S=2×2÷2=2cm2;
当x=4cm时,S=6×6÷2-4×4÷2=10cm2;
当x=10cm时,S=2×2÷2=2cm2.
故答案为:2cm2;10cm2;2cm2.
 (2)如图所示:过点C做CM⊥AB于点M.
(2)如图所示:过点C做CM⊥AB于点M.
当4<x<6时,
梯形GDMC的面积=
(GD+CM)×DM
=
(x+6)(6-x)
=-
x2+18,
梯形CMEF的面积=
(EF+CM)×ME
=
[12-(x+2)+6][(x+2)-6]
=
(16-x)(x-4)
=-
x2+10x-32,
S=梯形GDMC的面积+梯形CMEF的面积=(-
x2+18)+(-
x2+10x-32)=-x2+10x-14;
(3)当x=4时,S=10cm2,
所以当S=11cm2时,x必然大于4,即-x2+10x-14=11,
解得x1=x2=5,
所以当x=5cm时,阴影部分面积为11cm2.
当x=4cm时,S=6×6÷2-4×4÷2=10cm2;
当x=10cm时,S=2×2÷2=2cm2.
故答案为:2cm2;10cm2;2cm2.
 (2)如图所示:过点C做CM⊥AB于点M.
(2)如图所示:过点C做CM⊥AB于点M.当4<x<6时,
梯形GDMC的面积=
| 1 |
| 2 |
=
| 1 |
| 2 |
=-
| 1 |
| 2 |
梯形CMEF的面积=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=-
| 1 |
| 2 |
S=梯形GDMC的面积+梯形CMEF的面积=(-
| 1 |
| 2 |
| 1 |
| 2 |
(3)当x=4时,S=10cm2,
所以当S=11cm2时,x必然大于4,即-x2+10x-14=11,
解得x1=x2=5,
所以当x=5cm时,阴影部分面积为11cm2.
点评:考查了相似形综合题,涉及的知识点有:直角三角形的面积,矩形的性质,梯形的面积,分类思想的应用,方程思想的应用,综合性较强,难度中等.

练习册系列答案
相关题目
 已知,如图D是△ABC中BC边延长线上一点,DF⊥AB交AB于F,交AC于E,∠A=46°,∠D=50°.求∠ACB的度数.
已知,如图D是△ABC中BC边延长线上一点,DF⊥AB交AB于F,交AC于E,∠A=46°,∠D=50°.求∠ACB的度数. 如图,已知点E在直线AB外,请用三角板与直尺画图,并回答第(3)题:
如图,已知点E在直线AB外,请用三角板与直尺画图,并回答第(3)题: 如图:平行四边形ABCD的周长为16cm,AC,BD交于点O,OE⊥AC交AD于E,求△DCE的周长.
如图:平行四边形ABCD的周长为16cm,AC,BD交于点O,OE⊥AC交AD于E,求△DCE的周长. 已知:如图DE∥BC,且∠1=∠3,试说明:FG∥DC.(请把下列解题过程补充完整并在括号中注明理由)
已知:如图DE∥BC,且∠1=∠3,试说明:FG∥DC.(请把下列解题过程补充完整并在括号中注明理由)