题目内容
11.计算:(1)$\frac{x}{{x}^{2}+x}$÷$\frac{{x}^{2}+x-2}{{x}^{2}-1}$+$\frac{x+1}{x+2}$;
(2)5$\sqrt{12}$÷$\frac{1}{2}\sqrt{48}$-6$\frac{2}{3}$×$\sqrt{2}$;
(3)(3+$\sqrt{5}$)(3-$\sqrt{5}$)-($\sqrt{3}-1$)2;
(4)$\sqrt{a}$-2$\sqrt{a-b}$+$\sqrt{160}$-a$\sqrt{\frac{b}{a}}$(a>0,b>0);
(5)($\frac{x}{x-y}$-1)÷$\frac{{y}^{2}}{x+y}$•(x-$\frac{{x}^{2}}{x+y}$)
分析 (1)首先把分式的分子与分母分解因式,把除法转化为乘法,计算乘方,然后进行加减计算即可;
(2)首先化简二次根式,然后进行乘除计算,然后进行加减即可;
(3)首先利用平方差公式和完全平方公式计算,然后合并同类二次根式即可;
(4)化简二次根式即可求解;
(5)首先对括号内的分式进行计算,把除法转化为乘法,然后进行乘法计算即可.
解答 解:(1)原式=$\frac{x}{x(x+1)}$•$\frac{(x+1)(x-1)}{(x+2)(x-1)}$+$\frac{x+1}{x+2}$=$\frac{1}{x+2}$+$\frac{x+1}{x+2}$=$\frac{x+2}{x+2}$=1;
(2)原式=10$\sqrt{3}$÷2$\sqrt{3}$-$\frac{20\sqrt{2}}{3}$=5-$\frac{20\sqrt{3}}{3}$;
(3)原式=9-5-(3-2$\sqrt{3}$+1)=9-5-3+2$\sqrt{3}$-1=2$\sqrt{3}$;
(4)原式=$\sqrt{a}$-2$\sqrt{a-b}$+4$\sqrt{10}$-$\sqrt{ab}$;
(5)原式=$\frac{x-x+y}{x-y}$•$\frac{x+y}{{y}^{2}}$•$\frac{x(x+y)-{x}^{2}}{x+y}$=$\frac{y}{x-y}$•$\frac{x+y}{{y}^{2}}$•$\frac{{y}^{2}}{x+y}$=$\frac{y}{x-y}$.
点评 本题考查的是二次根式的混合运算,在进行此类运算时,一般先把二次根式化为最简二次根式的形式后再运算.

练习册系列答案
相关题目
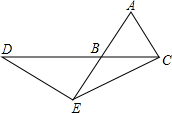 等边三角形ABC的边长为1,点D在直线BC上,点E在直线AB上,且AE=2.若△ECD是以CD为底的等腰三角形,则CD的长为3.
等边三角形ABC的边长为1,点D在直线BC上,点E在直线AB上,且AE=2.若△ECD是以CD为底的等腰三角形,则CD的长为3.