题目内容
6.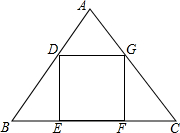 如图,正方形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,已知BC=6,△ABC的面积为9,则正方形DEFG的面积为4.
如图,正方形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,已知BC=6,△ABC的面积为9,则正方形DEFG的面积为4.
分析 由DG∥BC得△ADG∽△ABC,利用相似三角形对应边上高的比等于相似比,列方程求解.
解答 解:作AH⊥BC于H,交DG于P,如图所示: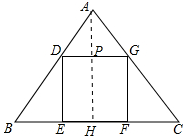
∵△ABC的面积=$\frac{1}{2}$BC•AH=9,BC=6,
∴AH=3,
设正方形DEFG的边长为x.
由正方形DEFG得,DG∥EF,即DG∥BC,
∵AH⊥BC,
∴AP⊥DG.
由DG∥BC得△ADG∽△ABC
∴$\frac{DG}{BC}=\frac{AP}{AH}$.
∵PH⊥BC,DE⊥BC
∴PH=ED,AP=AH-PH,
即$\frac{DG}{BC}=\frac{AH-PH}{AH}$,
由BC=6,AH=3,DE=DG=x,
得$\frac{x}{6}=\frac{3-x}{3}$,
解得x=2.
故正方形DEFG的面积=22=4;
故答案为:4.
点评 本题考查了相似三角形的判定与性质、正方形的性质.关键是由平行线得到相似三角形,利用相似三角形的性质列方程.

练习册系列答案
相关题目
1.目前节能灯在城市已基本普及,某商场计划购进甲、乙两种节能灯共1200只,这两种节能灯的进价、售价如下表:
(1)如何进货,进货款恰好为46000元?
(2)为确保乙型节能灯顺利畅销,在(1)的条件下,商家决定对乙型节能灯进行打折出售,且全部售完后,乙型节能灯的利润率为20%,请问乙型节能灯需打几折?
| 进价(元/只) | 售价(元/只) | |
| 甲型 | 25 | 30 |
| 乙型 | 45 | 60 |
(2)为确保乙型节能灯顺利畅销,在(1)的条件下,商家决定对乙型节能灯进行打折出售,且全部售完后,乙型节能灯的利润率为20%,请问乙型节能灯需打几折?
15.如果2x2+ax-2y+7-(bx2-2x+9y-1)的值与x的取值无关,则-a-2b的值为( )
| A. | 3 | B. | 1 | C. | 2 | D. | -2 |
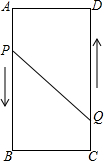 A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.
A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动. 如图,长、宽分别为a、b的长方形硬纸片拼成一个“带孔”正方形,利用面积的不同表示方法,写出一个等式(a+b)2=(a-b)2+4ab.
如图,长、宽分别为a、b的长方形硬纸片拼成一个“带孔”正方形,利用面积的不同表示方法,写出一个等式(a+b)2=(a-b)2+4ab.
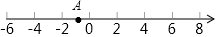 如图,已知点A在数轴上,从点A出发,沿数轴向右移动3个单位长度到达点C,点B所表示的有理数是5的相反数,按要求完成下列各小题.
如图,已知点A在数轴上,从点A出发,沿数轴向右移动3个单位长度到达点C,点B所表示的有理数是5的相反数,按要求完成下列各小题.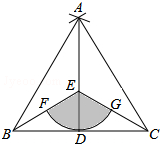 如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E是AD上一点(不与点A,D重合),连接BE,CE,以点E为圆心,ED长为半径画弧,分别交BE,CE于点F,G,若BC=6,∠EBC=45°,则图中阴影部分的面积为$\frac{9}{2}$π.
如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E是AD上一点(不与点A,D重合),连接BE,CE,以点E为圆心,ED长为半径画弧,分别交BE,CE于点F,G,若BC=6,∠EBC=45°,则图中阴影部分的面积为$\frac{9}{2}$π.