题目内容
3.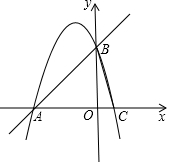 如图,抛物线y=-x2+bx+c经过A(-3,0)、B(0,3)两点,与x轴交于另一点C.
如图,抛物线y=-x2+bx+c经过A(-3,0)、B(0,3)两点,与x轴交于另一点C.(1)求直线AB的解析式;
(2)求△ABC的面积.
分析 (1)用待定系数法可得AB的解析式,首先设AB的解析式为:y=kx+b,再将A、B点坐标代入,解得k,b,再代入即可;
(2)将B、C点的坐标代入抛物线的解析式,解得b,c,利用抛物线与x轴的交点坐标,解得C点坐标,求得AC的长,易得△ABC的面积.
解答 解:(1)解:设直线AB的解析式为y=kx+b,
将A、B点坐标代入得,
$\left\{\begin{array}{l}{0=-3k+b}\\{3=b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$,
∴直线AB的解析式为:y=x+3;
(2)将B、C点的坐标代入抛物线的解析式得,
$\left\{\begin{array}{l}{0={-(-3)}^{2}-3b+c}\\{3=c}\end{array}\right.$
解得:$\left\{\begin{array}{l}{b=-2}\\{c=3}\end{array}\right.$,
∴抛物线的解析式为:y=-x2-2x+3,
令y=0,则0=-x2-2x+3,
x1=-3,x2=1,
所以C点的坐标为:(1,0),
∴|AC|=4,
∴S△ABC=$\frac{1}{2}×|AC|{×y}_{B}$=$\frac{1}{2}×4×3$=6.
点评 本题主要考查了待定系数法求解析式,解得C点的坐标是解答此题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
13.超市出售的三种品牌月饼袋上,分别标有质量为(300±5)g,(300±10)g,(300±15)g的字样,从中任意拿出两袋,它们的质量最多相差( )
| A. | 10g | B. | 20g | C. | 30g | D. | 40g |
11. 将正整数按如图所示的位詈顺序排列:根据排列规律,则2016应在( )
将正整数按如图所示的位詈顺序排列:根据排列规律,则2016应在( )
 将正整数按如图所示的位詈顺序排列:根据排列规律,则2016应在( )
将正整数按如图所示的位詈顺序排列:根据排列规律,则2016应在( )| A. | A位置 | B. | B位置 | C. | C位置 | D. | D位置 |
18.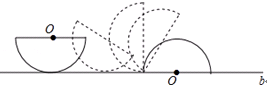 如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于( )
如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于( )
 如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于( )
如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于( )| A. | 5π | B. | 2.5π | C. | 5+2.5π | D. | 10 |
8.已知反比例函数y=(a-2)${x^{{a^2}-4a+2}}$的图象位于第二、四象限,则a的值为( )
| A. | 1 | B. | 3 | C. | -1 | D. | -3 |
15.如果y=$\sqrt{x-4}$+$\sqrt{4-x}$+1,则2x+y的平方根是( )
| A. | 9 | B. | ±9 | C. | 3 | D. | ±3 |
12.某班6个同学体育课三步上篮的投篮数如下:5、5、6、7、7、8.这组数据的中位数是( )
| A. | 7 | B. | 6 | C. | 6.5 | D. | 5 |
13.三角形两边长分别为4和6,第三边的长是方程x2-14x+40=0的两根,则该三角形的周长为( )
| A. | 14 | B. | 16 | C. | 20 | D. | 14或20 |