题目内容
14.用适当的方法解方程:(1)x2-4=0
(2)-2x2+3x+1=0
(3)x2-3x-4=0
(4)(x+2)2-10(x+2)+25=0.
分析 (1)原方程变形为x2=4,直接开平方法可得.
(2)利用公式法解方程.
(3)十字相乘法求解可得;
(4)换元法求解可得.
解答 解:(1)移项得:x2=4,
解得x1=2,x2=-2.
(2)由原方程,得:2x2-3x-1=0,
∵a=2,b=-3,c=-1,
∴△=b2-4ac=(-3)2-4×2×(-1)=17>0,
则x=$\frac{3±\sqrt{17}}{4}$,
∴x1=$\frac{3+\sqrt{17}}{4}$,x2=$\frac{3-\sqrt{17}}{4}$.
(3)方程左边因式分解得:(x+1)(x-4)=0,
∴x+1=0或x-4=0,
解得:x=-1或x=4.
(4)令x+2=a,则方程可变形为:a2-10a+25=0,
∴(a-5)2=0,
解得a=5,
即x+2=5,
∴x=3.
点评 本题主要考查解一元二次方程的能力,根据方程的不同特点灵活选择适当方法是解题的关键.

练习册系列答案
相关题目
5. 如图,在菱形ABCD中,∠BCD=80°,BC的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠ADF等于( )
如图,在菱形ABCD中,∠BCD=80°,BC的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠ADF等于( )
 如图,在菱形ABCD中,∠BCD=80°,BC的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠ADF等于( )
如图,在菱形ABCD中,∠BCD=80°,BC的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠ADF等于( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
4.对称轴是直线x=-2的抛物线是( )
| A. | y=-2x2-2 | B. | y=2x2-2 | C. | y=-(x+2)2 | D. | y=-(x-2)2 |
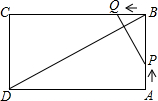 如图:矩形ABCD中,点P从A出发经过1分钟沿AB运动可以到达B点,点Q从B出发经过1分钟沿BC运动可以到达C点,AB=5,BC=10,若P、Q同时出发,问经过多长时间PQ与BD垂直?
如图:矩形ABCD中,点P从A出发经过1分钟沿AB运动可以到达B点,点Q从B出发经过1分钟沿BC运动可以到达C点,AB=5,BC=10,若P、Q同时出发,问经过多长时间PQ与BD垂直? 如图,在⊙O中,∠ACB=∠D=60°,AC=3,则⊙O的直径为9.
如图,在⊙O中,∠ACB=∠D=60°,AC=3,则⊙O的直径为9. 如图,在矩形ABCD中,AB=4,BC=8,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则CE的长为( )
如图,在矩形ABCD中,AB=4,BC=8,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则CE的长为( )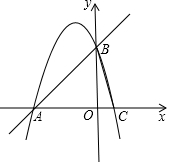 如图,抛物线y=-x2+bx+c经过A(-3,0)、B(0,3)两点,与x轴交于另一点C.
如图,抛物线y=-x2+bx+c经过A(-3,0)、B(0,3)两点,与x轴交于另一点C.