题目内容
19. AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K,且KG2=KD•KE.
AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K,且KG2=KD•KE.(1)求证:AC∥EF;
(2)若sinE=$\frac{3}{5}$,AC=2$\sqrt{10}$,求HK的长.
分析 (1)由已知条件证出△DKG∽△GKE,得出∠DGK=∠E,再由同弧所对的圆周角相等得出∠DGK=∠ACD,得出∠E=∠ACD,即可证出平行线;
(2)连接BG,先由弦切角定理得出∠1=∠2,再证出AC=KC,由三角函数求出CH,即可得出HK.
解答 (1)证明:连接DG,如图所示: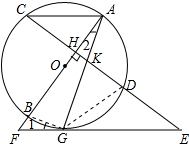 ∵KG2=KD•KE,
∵KG2=KD•KE,
∴KG:KD=KE:KG,
∵∠DKG=∠GKE,
∴△DKG∽△GKE,
∴∠DGK=∠E,
∵∠DGK=∠ACD,
∴∠E=∠ACD,
∴AC∥EF;
(2)连接BG,如图所示:
则∠1=∠2,∠AGB=90°,
∴∠1+∠AGE=90°,
由(1)得:∵CD⊥AB,
∴∠AHC=90°,∠E=∠ACD,
∴∠2+∠AKC=90°,
∴∠AKC=∠AGE,
∵AC∥EF,
∴∠CAG=∠AGE,
∴∠CAG=∠AKC,
∴AC=KC,sin∠ACD=$\frac{AH}{AC}$=$\frac{3}{5}$,
∴AH=$\frac{3}{5}$AC=$\frac{6\sqrt{10}}{5}$,
∴CH=$\frac{4}{5}$AC=$\frac{8\sqrt{10}}{5}$,
∴HK=KC-CH=AC-CH=$\frac{2\sqrt{10}}{5}$.
点评 本题考查了切线的性质、相似三角形的判定与性质、平行线的判定与性质、等腰三角形的判定以及三角函数;本题有一定难度,特别是(2)中,需要通过作辅助线证明等腰三角形和运用三角函数才能求出结果.

练习册系列答案
相关题目
4.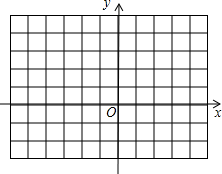 已知三角形A′B′C′是由三角形ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
已知三角形A′B′C′是由三角形ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
(1)填空:a=-3,b=3,c=4;
(2)画出三角形ABC和三角形A′B′C′.
 已知三角形A′B′C′是由三角形ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
已知三角形A′B′C′是由三角形ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:| 三角形ABC | A(a,2) | B(-5,1) | C(-2,0) |
| 三角形A′B′C′ | A′(3,4) | B′(1,b) | C′(c,2) |
(2)画出三角形ABC和三角形A′B′C′.
11.如果ab>0,且ac=0,那么直线y=-$\frac{a}{b}$x+c一定通过( )
| A. | 第一、二象限 | B. | 第三、四象限 | C. | 第一、三象限 | D. | 第二、四象限 |
9.线段CD是由线段AB平移得到的,点A(1,8)的对应点C(-3,0),则点B(4,7)的对应点D的坐标为( )
| A. | (-1,0) | B. | (6,9) | C. | (0,-1) | D. | (9,6) |
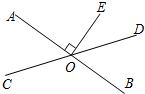 如图,直线AB.CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,则∠AOC=52 度.
如图,直线AB.CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,则∠AOC=52 度.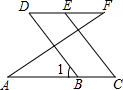 如图,已知∠A=∠F,∠C=∠D,按图填空,括号内注明理由
如图,已知∠A=∠F,∠C=∠D,按图填空,括号内注明理由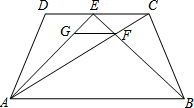 如图,在梯形ABCD中,AB∥CD,AD=BC,E是CD的中点,BE交AC于F,过点F作FG∥AB,交AE于点G.
如图,在梯形ABCD中,AB∥CD,AD=BC,E是CD的中点,BE交AC于F,过点F作FG∥AB,交AE于点G.