题目内容
2.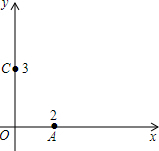 已知:A,B都是x轴上的点,点A的坐标是(2,0),且线段AB的长等于4,点C的坐标是(0,3).
已知:A,B都是x轴上的点,点A的坐标是(2,0),且线段AB的长等于4,点C的坐标是(0,3).(1)直接写出点B的坐标;
(2)求直线BC的函数表达式.
分析 (1)根据A的坐标和AB=4,分B在A点的左边和右边两种情况求得B的坐标;
(2)根据待定系数法求得即可.
解答 解:(1)∵A,B都是x轴上的点,点A的坐标是(2,0),且线段AB的长等于4,
∴B(6,0)或(-2,0);
(2)设直线BC的解析式为y=kx+b,
∵直线经过C(0,3),
∴直线BC的解析式为y=kx+3,
当B(6,0)时,0=6k+3,解得k=-$\frac{1}{2}$,
当B(-2,0)时,0=-2k+3,解得k=$\frac{3}{2}$,
∴直线BC的函数表达式为y=-$\frac{1}{2}$x+3或y=$\frac{3}{2}$x+3.
点评 本题考查了待定系数法求一次函数的解析式,根据题意求得B的两个坐标是解题的关键.

练习册系列答案
相关题目
12.当x=2时,代数式ax3+bx+1值为3,那么当x=-2时,代数式ax3+bx+1的值是 ( )
| A. | -3 | B. | 1 | C. | -1 | D. | 2 |
17.将正整数1,2,3,…从小到大按下面规律排列,则第i行第j列的数为n(i-1)+j(用i,j表示).
| 第1列 | 第2列 | 第3列 | … | 第n列 | |
| 第1行 | 1 | 2 | 3 | … | n |
| 第2行 | n+1 | n+2 | n+3 | … | 2n |
| 第3行 | 2n+1 | 2n+2 | 2n+3 | … | 3n |
| … | … | … | … | … | … |
7.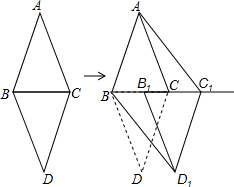 如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=6cm,BC=4cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,那么平移的距离为( )
如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=6cm,BC=4cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,那么平移的距离为( )
 如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=6cm,BC=4cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,那么平移的距离为( )
如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=6cm,BC=4cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,那么平移的距离为( )| A. | 14cm | B. | 16cm | C. | 18cm | D. | 20cm |
14.下列图形是轴对称而不是中心对称图形的是( )
| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 等边三角形 |
 如图,P为菱形ABCD的对角线上一点,PE丄AB于点E,PF丄AD于点F,PF=6
如图,P为菱形ABCD的对角线上一点,PE丄AB于点E,PF丄AD于点F,PF=6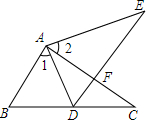 如图所示,点E在△ABC外部,点D在BC边上.DE交AC于F,若∠1=∠2,∠E=∠C,AE=AC,求证:△ABC≌△ADE.
如图所示,点E在△ABC外部,点D在BC边上.DE交AC于F,若∠1=∠2,∠E=∠C,AE=AC,求证:△ABC≌△ADE.