题目内容
通过对代数式的适当变形，求出代数式的值．
（1）若x+y=4，xy=3，求（x-y）2，x2y+xy2的值．
（2）若x=
+
，y=
-
，求x2-xy+y2的值．
（3）若x2-5x=3，求（x-1）（2x-1）-（x+1）2+1的值．
（4）若m2+m-1=0，求m3+2m2+2014的值．
（1）若x+y=4，xy=3，求（x-y）2，x2y+xy2的值．
（2）若x=
| 5 |
| 7 |
| 7 |
| 5 |
（3）若x2-5x=3，求（x-1）（2x-1）-（x+1）2+1的值．
（4）若m2+m-1=0，求m3+2m2+2014的值．
考点：整式的混合运算—化简求值
专题：
分析：（1）将（x-y）2通过配方法转化成（x+y）2，x2y+xy2因式分解即可；
（2）利用配方法转化成=（x+y）2-3xy即可；
（3）根据整式的乘法把式子展开即可；
（4）先把m2+m-1=0，变形为m2=1-m．把m3+2m2+2014变形为m2（m+2）+2014=（1-m）（m+2）+2014即可；
（2）利用配方法转化成=（x+y）2-3xy即可；
（3）根据整式的乘法把式子展开即可；
（4）先把m2+m-1=0，变形为m2=1-m．把m3+2m2+2014变形为m2（m+2）+2014=（1-m）（m+2）+2014即可；
解答：解：（1）（x-y）2=x2-2xy+y2=x2+2xy+y2-4xy=（x+y）2-4xy42-4×3=4，
x2y+xy2=xy（x+y）=3×4=12，
（2）x2-xy+y2=（x+y）2-3xy=（
+
+
-
）2-3（
+
）（
-
）=（2
）2-3×2=28-6=22
（3）（x-1）（2x-1）-（x+1）2+1=2x2-3x+1-（x2+2x+1）+1=x2-5x+1=3+1=4
4）由m2+m-1=0，得m2=1-m．把m3+2m2+2014=m2（m+2）+2014=（1-m）（m+2）+2014=m-1-m+2+2014
x2y+xy2=xy（x+y）=3×4=12，
（2）x2-xy+y2=（x+y）2-3xy=（
| 5 |
| 7 |
| 7 |
| 5 |
| 5 |
| 7 |
| 7 |
| 5 |
| 7 |
（3）（x-1）（2x-1）-（x+1）2+1=2x2-3x+1-（x2+2x+1）+1=x2-5x+1=3+1=4
4）由m2+m-1=0，得m2=1-m．把m3+2m2+2014=m2（m+2）+2014=（1-m）（m+2）+2014=m-1-m+2+2014
点评：此题考查了学生的应用能力，解题时要注意配方法的步骤．注意在变形的过程中不要改变式子的值．
练习册系列答案
互动英语系列答案
相关题目
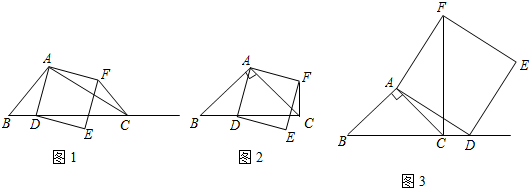
如图已知△ABC，请你用直尺和圆规作图，作一个三角形，使它和△ABC全等．（要求用尺规作图，不必写你是如何作的，但是要保留作图时留下的作图痕迹）